Gridded
Minimization with PERPLE_X
THIS HTML IS UNDER CONSTRUCTION AND MAY BE
ILLEGIBLE ON BROWSERS OTHER THAN MICROSOFT EXPLORER
WARNING! NOT ONLY IS THIS PAGE UNDER CONSTRUCTION, BUT IT IS ALSO OUT-OF-DATE: SINCE JANUARY 2002, VERTEX AND BUILD HAVE BEEN USING A 2-DIMENSIONAL MULTILEVEL GRID STRATEGY AS OPPOSED TO THE 1-DIMENSIONAL STRATEGY DESCRIBED HERE, THE ESSENCE OF THE 2D STRATEGY IS SIMILAR TO THE 1D STRATEGY, SO THIS DOCUMENT IS USEFUL FOR UNDERSTANDING THE BASIC CONCEPT.
Contents
IntroductionSchematic Figure
Multi-Level
Grid and Compression Strategy:
BUILD Prompts
The basis of the optimization strategy used within Perple_X is the pseudocompound approximation. In this approximation, each
solution phase is represented by a series of stoichiometric compounds (pseudocompounds) that descretize
the possible composition of the solution (Connolly & Kerrick
1987, Connolly 1990, Connolly & Petrini 2002). Because of this approximation, the
continuous phase fields of a pseudosection (or any
other phase diagram derivative) are also discretized,
a representation referred to as a “polygonalized”
phase diagram section (Fig 1a, Connolly & Petrini 2002). Polygonalized
phase diagram sections can be computed by two methods within Perple_X, the
method is specified by the users response to the BUILD
prompt:
Specify computational mode: 1 - Unconstrained minimization [default] 2 - Constrained minimization on a grid 3 - Output pseudocompound data 4 - Phase fractionation calculations
The default mode [1] (Connolly & Petrini 2002) essentially consists of tracing the edges of
each field of a polygonalized pseudosection
(Fig 1a). The alternative mode [2] is gridded minimization (Fig 1d). In gridded
minimization the polygonalized pseudosection
is mapped from free energy minimizations done on a 1- or 2-dimensional grid,
whereby the stable assemblage determined at each grid point is assumed to be
stable over the area associated with the grid point.
Each mode has features that makes
it preferable for certain problems, for preliminary calculations I prefer gridded minimization because it is simpler to use and can
be run at low resolution to provide rough results quickly. Other pros and cons
of the default mode (unconstrained minimization) vs gridded minimization are:
·
The default mode requires the program
POLYGON, this program is difficult to compile on anything other than a PC, and
is therefore not available to most Mac and UNIX users.
·
Gridded
minimization can be used to compute pseudosections as
a function of any variable of the system, most notably
it can be used to compute phase diagram sections as a function of the bulk
composition of the system. The default mode can only be used to compute (at
least explicitly) sections as a function of a systems
environmental variables.
·
In the default mode VERTEX may not be
able to trace all the edges of a polygon resulting in a data-less hole in the
section (see the pseudosection tutorial). Such holes
are extraordinarily rare with gridded minimization.
·
Gridded
minimization may be run with very large numbers of pseudocompounds
(>106), so it is possible to resolve phase compositions more
accurately. In principle this is possible with unconstrained minimization as
well, but it involves changing more parameters.
·
Properties such as density or enthalpy
vary continuously within each polygonal field of a pseudosection, such
variations are estimated in WERAMI from low order derivatives. In the default
mode, this estimation may become inaccurate if the polygonal fields of a
diagram are large. In gridded minimization, the
extent of extrapolation is limited by the grid spacing. Thus when such
properties are of interest gridded minimization is
preferable. To further minimize extrapolation errors, the compression strategy
(detailed below) used by VERTEX should be turned off.
·
Gridded
minimization compounds the error associated with the polygonalization
of a pseudosection, because the polygonalized
phase diagram is resolved with the finite accuracy of the grid. The default
mode computes the polygonalized diagram exactly (for
practical purposes).
·
The gridded
minimization strategy cannot distinguish univariant
and invariant phase fields from small lower variance phase fields. The default
mode can, in principle, make these distinctions, but it may make erroneous
assignments because of the pseudocompound
approximation.
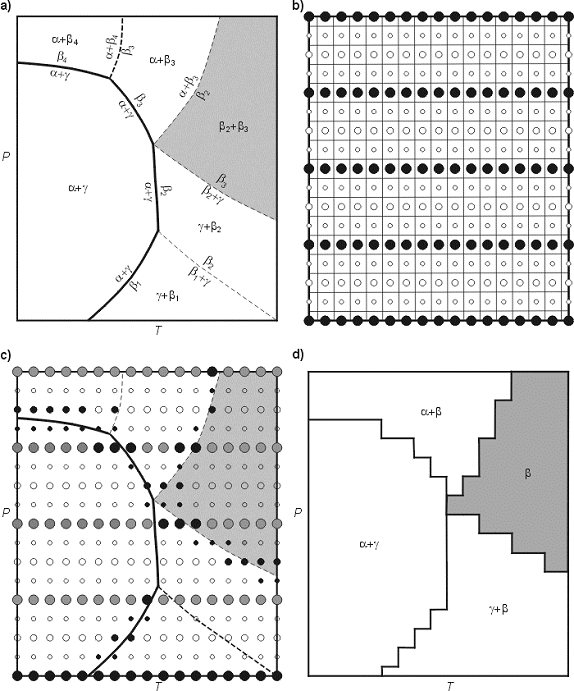Figure 1: a) Schematic polygonalized phase diagram section as would be computed
with the default mode for pseudosection calculations
in VERTEX. b) The grid defined for gridded minimization
by the parameter choice JLOW = 4, JLEV = 3, and XLOOP = 17. The filled circles
define the lowest level of the grid, the open circles
represent grid points that are activated only if changes occur between adjacent
nodes of the low level grid. c) Filled points indicate the 107 grid
points (out of the total of 289 points possible in b) that would be
activated during gridded minimization of the polygonalized pseudosection (in a),
the 41 lightly shaded points would be discarded during compression. d) The
final pseudosection as reconstructed from the 66 grid
points retained after compression.
The Multi-Level Grid, BUILD Prompts, and Compression Strategy
VERTEX uses a 1-dimensional multi-level mapping strategy
to compute pseudosections. This strategy begins with
the calculation of phase relations on a low resolution grid, if phase relations
change between two nodes of the low resolution grid, the location of the phase
boundary is then refined by bisection until the highest resolution of the grid is
achieved. This procedure is currently implemented in only one direction (i.e.,
along the Y-axis), thus the grid spacing in the orthogonal direction must be
chosen to give the maximum resolution required. The parameters for that define
the grid are entered by the user in BUILD through the following dialog:
Select grid refinement mode: 1 - Refine only true phase boundaries [default]. 2 - Refine all phase boundaries. This prompt determines what
features will be resolved at the highest level of resolution. Mode 2 should
always be used if the properties of the stable phases within the various fields
of the diagram are of interest. With
reference to the polygonalized pseudosection
of Fig 1a, all the curves of the pseudosection with
the exception of the pseudounivariant fields b3 = a + b4 and b2 = b1 + g, are true phase boundaries. The pseudounivariant fields b3 = a + b4 and b2 = b1 + g are not true phase boundaries
because the lie within the true divariant fields of a + b and b + g, these boundaries
are important if, for example, the user wishes to know the composition of b as
a function of pressure and temperature, but they are unimportant if the user is
only concerned with determining the pressure-temperature conditions over which
the various true phase assemblages are stable.
2 The resolution of the y-axis grid is determined by the number oflevels (JLEV) and the resolution at the lowest level (JLOW), such
that the maximum resolution is equivalent to that obtained on a
single level grid with (1+(JLOW-1)*2**(JLEV-1))**2 nodes. To force
VERTEX to use a single level grid, set JLEV=1 and set JLOW equalto the number of nodes along the y-axis of the grid.
Enter lowest resolution (JLOW) for the grid (2<JLOW<1024) [default = 10]: JLOW is the minimum number of
regularly spaced nodes along the vertical axis. The danger of using the lowest
value possible (2) is that a phase field that protrudes into a larger
phase field will not be identified if the protrusion occurs between two nodes
of the low resolution grid at which the larger field is stable. There is no
rule for the best choice of JLOW as it depends on the scale of the diagram and
the heterogeneity of its phase fields. I generally use values between 10 and
25.
The value chosen here gives the
nodes along the vertical axis depicted by the large filled circles in Fig 1b.
VERTEX establishes the stable phases of the system at every point of the low
resolution grid.
5
Enter the number of levels (JLEV) for the grid (0<JLEV<10) [default = 5]: The value specified here
determines the highest resolution of the grid, i.e. (Ymax
– Ymin)/(JLOW –
1)(JLEV-1). All features that change between two grid points at the
lowest resolution of the grid are resolved at this level of resolution.
Specifying 3 here creates a grid with two sub levels indicated by the medium
and small open circles in Fig 1b. Fig 1c shows the high resolution grid points
that would be tested by VERTEX as a result of the grid refinement strategy.
With reference to the example of Fig 1, VERTEX would begin by calculating phase
relations at the lowest level of resolution by incrementing pressure at the
lowest temperature. The phase relations would change at this level at the last
grid point due to the univariant field a + g = b4, this change would cause VERTEX to calculate the stable
assemblage on the grid at the next level of resolution half between the last
two nodes of the low resolution grid. At this intermediate grid point the
assemblage is the same as at the last grid point of the low resolution grid,
therefore VERTEX “knows” that the phase boundary must be located below the
intermediate grid point and activates the grid point at the highest level of
resolution so that the univariant field a + g = b4 is located with an accuracy corresponding to the finest
spacing of the grid.
3
These parameters define a multilevel grid equivalent to a regulargrid with 17 nodes in the y-direction, change the parameters (y/n)?
n
Specify the number of grid nodes in the x-direction [<1024 default = 17,the maximum resolution in the y-direction]:
The grid spacing in the
x-direction is constant (i.e., a single level grid) and can be specified
independently of the gridding in the y-direction. By
default BUILD sets the x-resolution equal to the maximum resolution in the
y-direction.
17
The multilevel grid strategy can result in a substantial
reduction in the number of minimizations necessary to map the phase fields of a
pseudosection, but despite this many of the
minimizations are redundant. This is evident from consideration of the first
column of the grid in Fig 1c; where although VERTEX would do eight
minimizations in this column (the filled grid points), the phase relations can
be established from the stable assemblage at the base of the column and the
grid points on either side of the phase field boundary a + g
= b4. To reduce the
size of output files, by default VERTEX discards any data obtained at grid
points that are not necessary to define the stable phase relations of the
diagram (i.e., the shaded points in Fig 1c). For the example in Figure 1, this
compression reduces the total number of grid points to 66 out of the total of
289 theoretically possible and 107 actually used. The final pseudosection
that would be obtained from this data with PSVDRAW (Fig 1d) is much coarser
than the polygonalized phase diagram that would be
obtained by the default mode (Fig 1a). However, it is possible to use such fine
grids in practice that there is little difference between pseudosections
constructed by either method.
Turning Compression Off
Physical properties such as density and seismic
velocities may vary continuously within each polygonal element of a polygonalized pseudosection. Normally
this variation is estimated in WERAMI (the program used to recover this
information) by extrapolation from the retained grid points assuming the first,
and for some properties higher order derivatives, of the property of interest
are constant within the relevant polygonal field. In some instances,
particularly when a single polygonal field spans a large pressure or
temperature interval, this means of estimation may lead to significant errors
(such errors are usually manifest by irregular variation across what should be
a continuous phase field). To minimize
such complications, compression can be turned off in VERTEX so that physical
properties are sampled and output at relatively regular intervals. To turn compression
off, the user must modify the input file created by BUILD so that the line:
1 JTEST, debug flag
reads:
3 JTEST, debug flag