!!!WARNING!!!
This tutorial is out-of-date, it was written for the 06 version of Perple_X. the best current tutorial for the calculation of phase diagram sections is the seismic velocity tutorial. Although the seismic velocity tutorial illustrates the extraction of seismic velocities from a phase diagram section, the basic calculation is typical of phase diagram section calculations. The tutorial here has not been removed because components of this tutorial illustrate features, e.g., the use of bulk compositions as independent variables for a phase diagram section, that are still pertinent to the current version of Perple_X and not addressed in other Perple_X tutorials.
IntroductionRunning BuildRunning VertexRunning PsvdrawUsing Werami to check and refine solution modelsFigures:Figure 1. Metapelite phase diagram section, high resolution, simplified melt modelFigure 2. Metapelite phase diagram section, low resolution, complete melt model
This is a bare bones tutorial intended to illustrate the construction of phase diagram sections with compositional variables by gridded minimization in Perple_X. The calculation outlined here is Perple_X example 19, which is briefly discussed in Connolly (2005). The calculation concerns melting phase relations along a Barrovian geothermal gradient for a metapelitic rock as a function of bulk water content. The type of calculation required for this example is a minor variation on the calculations described in the pseudosection and the seismic velocity tutorials. Novice users should refer to these tutorials for more complete explanation of the various prompts and methods. This tutorial covers two themes not covered in earlier tutorials: the grid compression prompt, and the use of WERAMI to refine the compositional parameters for solution models.

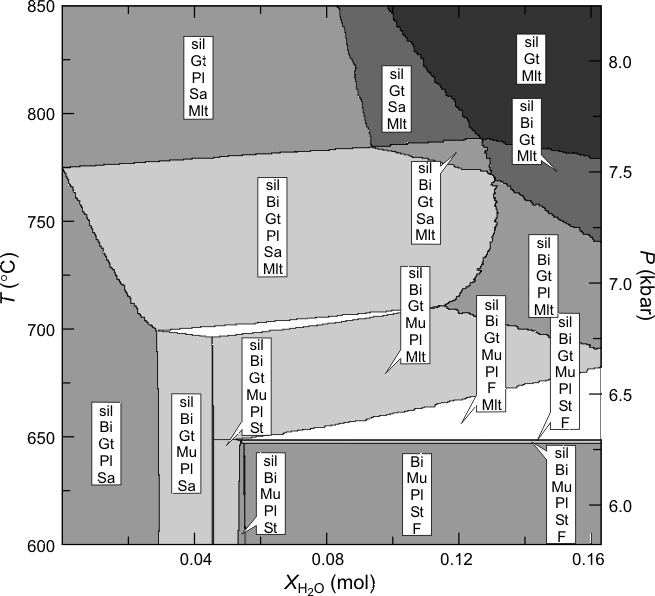
Figure 1. Phase relations along a Barrovian geotherm (25 K/km, Pressure indicated on the right-hand axis) as a function of water content for a pelitic composition (0.021 Na2O, 0.038 K2O, 0.008 CaO, 0.050 MgO, 0.096 FeO, 0.189 Al2O3, 1.021 SiO2 in molar units) modified from , the maximum molar water content represented on the diagram corresponds to 5 wt% H2O. For the calculation the melt model was simplified by excluding the anL, fo8L, fa8L and sil8L endmembers, this simplification is the primary reason for the differences between the high resolution calculation and the low resolution calculation made here (Figure 2). For the high resolution calculation, phase compositions where discretized with an accuracy of better than 0.03 mol% (generating 7×106 pseudocompounds) on a 5-level grid with 40x40 nodes at the lowest level (625x625 nodes at the highest level).
In the following sections the prompts from Perple_X programs are written in normal font; user responses are bold font; and interspersed explanatory comments are in red. Additional explanation on some prompts is available via the (help) links.
The user/BUILD dialog that defines the calculation is reproduced with commentary below:
C\jamie\Berple_X> build
NO is the default ([cr]) answer to all Y/N prompts (help)
Enter name of computational option file to be created, < 100 characters, left justified [default = in]: (help)
in19.dat
A copy of this file is at in19.dat
Enter thermodynamic data file name, left justified, [default = hp02ver.dat]: (help)
hp02ver.dat
The current data base components are:
NA2O MGO AL2O3 SIO2 K2O CAO TIO2 MNO FEO NIOO2 H2O CO2Transform them (Y/N)? (help)
n
Calculations with a saturated phase (Y/N)? (help)
The phase is: FLUID
Its compositional variable is: Y(CO2), X(O), etc.
n
In the current version of Perple_X H2O can be specified as a saturated phase or saturated component (despite warnings to the contrary in the solution model files and earlier tutorials).
Calculations with saturated components (Y/N)? (help)
y
**warning ver015** if you select > 1 saturated component, then the order you enter the components determines the saturation heirarchy and may effect your results (see Connolly 1990).
Select < 6 saturated components from the set:NA2O MGO SIO2 AL2O3 K2O CAO TIO2 MNO FEO
NIO O2 H2O CO2
Enter names, left justified, 1 per line, <cr> to finish:SIO2
Use chemical potentials, activities or fugacities as independent variables (Y/N)? (help)
n
Select thermodynamic components from the set:
NA2O MGO AL2O3 K2O CAO TIO2 MNO FEO NIOO2 H2O CO2
Enter names, left justified, 1 per line, <cr> to finish:AL2O3
FEO
MGO
CAO
K2O
NA2O
H2O
**warning ver016** you are going to treat a saturated (fluid) phase component as a thermodynamic component, this may not be what you want to do. (help)
Select fluid equation of state: (help)
0 - X(CO2) Modified Redlich-Kwong (MRK/DeSantis/Holloway)1 - X(CO2) Kerrick & Jacobs 1981 (HSMRK)2 - X(CO2) Hybrid MRK/HSMRK3 - X(CO2) Saxena & Fei 1987 pseudo-virial expansion4 - Bottinga & Richet 1981 (CO2 RK)5 - X(CO2) Holland & Powell 1991, 1998 (CORK)6 - X(CO2) Hybrid Haar et al 1979/CORK (TRKMRK)7 - f(O2/CO2)-f(S2) Graphite buffered COHS MRK fluid8 - f(O2/CO2)-f(S2) Graphite buffered COHS hybrid-EoS fluid9 - Max X(H2O) GCOH fluid Cesare & Connolly 199310 - X(O) GCOH-fluid hybrid-EoS Connolly & Cesare 199311 - X(O) GCOH-fluid MRK Connolly & Cesare 199312 - X(O)-f(S2) GCOHS-fluid hybrid-EoS Connolly & Cesare 199313 - X(H2) H2-H2O hybrid-EoS14 - EoS Birch & Feeblebop (1993)15 - X(H2) low T H2-H2O hybrid-EoS16 - X(O) H-O HSMRK/MRK hybrid-EoS17 - X(O) H-O-S HSMRK/MRK hybrid-EoS18 - X(CO2) Delany/HSMRK/MRK hybrid-EoS, for P > 10 kb19 - X(O)-X(S) COHS hybrid-EoS Connolly & Cesare 199320 - X(O)-X(C) COHS hybrid-EoS Connolly & Cesare 199321 - X(CO2) Halbach & Chatterjee 1982, P > 10 kb, hybrid-Eos22 - X(CO2) DHCORK, hybrid-Eos23 - Toop-Samis Silicate Melt24 - f(O2/CO2)-N/C Graphite saturated COHN MRK fluid 25 - H2O-CO2-NaCl Aranovich and Haefner 2004
5
The data base has P(bar) and T(K) as default independent potentials. Make one dependent on the other, e.g., as along a geothermal gradient (y/n)?
y
Here the problem is to calculate a phase diagram section along the conditions of a geothermal gradient.
Select dependent variable:
1 - P(bar) = f(T(K))
2 - T(K) = f(P(bar))
1
The dependence must be described by the polynomial
P(bar) = Sum (c(i) * [T(K)]^i, i = 0..n)
In Perple_X geothermal gradients are defined by a polynomial of the form
Y = c0 + c1 X1 + c2 X2 + ... + cn Xn
where Y is the dependent variable, X is the independent variable, c0 ... cn are the polynomial coefficients and n is the order of the polynomial. Once the user has chosen the dependent variable (P(bar) above), Perple_X uses the independent variable for all subsequent prompts and graphics. The only constraint on the independent variable is that it must increase or decrease continuously.
The next prompts define the geothermal gradient as a function of the independent variable (T); to this end, we assume a linear gradient (polynomial of order n=1) passing through P=0 bar at T=273 K.
Enter n (<5)
1
Enter c(0)-2651.16
Enter c(1)9.70588
Specify computational mode: (help)
1 - Unconstrained minimization [default]
2 - Constrained minimization on a grid
3 - Output pseudocompound data
4 - Phase fractionation calculations
Unconstrained optimization should be used for the calculation of composition, mixed variable, and Schreinemakers diagrams, it may also be used for the calculation of phase diagram sections for a fixed bulk composition. Gridded minimization can be used to construct phase diagram sections for both fixed and variable bulk composition. Gridded minimization is preferable for the recovery of phase and bulk properties.
2
Select y-axis variable:
1 - T(K)
2 - Composition X(C2) (user defined)
1
That you are not prompted for the X-variable may seem odd, but BUILD "knows" from the previous prompts that the only variables possible are now temperature and bulk composition. Since mode 2 calculations are for a 2-dimensional section, the diagram must have at least 1 compositional variable (yet to be defined), which by default is made the X-axis variable. This prompt now requests the Y-axis variable, which may be a second composition variable (as in an X-X diagram), or temperature as specified here.
Enter minimum and maximum values, respectively, for: T(K)
873 1123
In this mode VERTEX uses a multilevel grid to define true phase boundaries or pseudocompound assemblage boundaries, mode 1 is the most efficient, modes 2-4 should be selected if physicochemical properties are to be retrieved from the section.
Select grid refinement mode: (help)1 - Refine only true phase boundaries, compression on.2 - Refine only true phase boundaries, compression off [default].3 - Refine all phase boundaries, compression on.4 - Refine all phase boundaries, compression off. 2
This choice will resolve physical properties with the resolution of the lowest level grid (below this will be specified as a 40x40 grid). To explain this by example: in this calculation bulk water content will be made to vary along the X-axis from 0 to 5 wt%, thus for a 40x40 grid, bulk water content will vary in steps of 5/40ths. Because Perple_X does not currently interpolate composition this means that after the calculation if you ask (with WERAMI) what is stable at an arbitrary X-value, then the bulk water content of the assemblage returned may differ from the X value by as much as 5/40/2.
The resolution of the grid is determined by the number of levels (JLEV) and the resolution at the lowest level in the X- and Y-directions (ILOW and JLOW, respectively), such that the maximum resolution is equivalent to that obtained on a single level grid with 1+(ILOW-1)*2^(JLEV-1) nodes in the X-direction and 1+(JLOW-1)*2^(JLEV-1) nodes in the Y-direction. To force VERTEX to use a single level grid, set JLEV=1.
Enter the number of nodes (ILOW) in the X-direction for the lowest resolution grid (0<ILOW<2048) [default = 40]: (help)
40
Enter the number of nodes (JLOW) in the Y-direction for the lowest resolution grid (1<JLOW<2048) [default = 40]: (help)
40
Enter the number of levels (JLEV) for the grid (0<JLEV<10) [default = 4]: (help)
2
These parameters define a multilevel grid equivalent to a regular X-Y grid with 79 x 79 nodes, change the parameters (y/n)?
n
In this mode all thermodynamic components must be constrained, constrain saturated components also (Y/N)?
y
The next prompts are for the saturated component constraints. Answering no at any point completes the set of constraints.
Constrain component SIO2 (Y/N)?
y
Specify component amounts by weight (Y/N)?
y
The bulk composition of the system will be computed as:
C = C0*(1-X(C1)) + C1*X(C1)
where X(C1) varies between 0 and 1, and C0 and C1 are the compositions specified next.
Enter weight amounts of the components: (help)
AL2O3 FEO MGO CAO K2O NA2O H2O SIO2
to define the composition C0
19.25 6.91 2.03 0.46 3.58 1.30 0.0 61.37
Enter weight amounts of the components: (help)
AL2O3 FEO MGO CAO K2O NA2O H2O SIO2
to define the composition C1
19.25 6.91 2.03 0.46 3.58 1.30 4.995 61.37
Do you want a print file (Y/N)?
n
Enter the plot file name, < 100 characters, left justified [default = pl]: (help)
plot19
**warning ver013** phase femg-1 has null or negative composition and will be rejected from the composition space.
Exclude phases (Y/N)? (help)
n
Do you want to treat solution phases (Y/N)?
y
Enter solution model file name [default = solution_model.dat] left justified, < 100 characters: (help)
solution_model.dat
**warning ver025** 0 endmembers for MELTS(GS) The solution will not be considered.
...output abridged...
**warning ver025** 1 endmembers for Ep(HP) The solution will not be considered.
Select phases from the following list, enter 1 per line, left justified, [cr] to finish: (help)
MnBio(HP) Bio(HP) Chl(HP) MnChl(HP) O(SG) E(SG)
Omph(HP) Cpx(HP) melt(HP) pMELTS(G) Opx(HP) Pheng(HP)
Sapp(HP) GaHcSp T MnSt(HP) Ctd(HP) Carp
hCrd Sud(Livi) Sud Cumm Anth Gl
Tr TrTsPg(HP) GlTrTs GlTrTsPg feldspar Pl(h)
AnPl AbPl Ab(h) Ab Kf(h) Kf
San MaPa KN-Phen MuCel PaCel MuPa
Pa Mu O(HP) Cpx(l) Cpx(h) Mont
Sp(JR) Sp(GS) Sp(HP) Neph(FB) GrPyAlSp(B GrPyAlSp(G
Gt(HP) GrPyAl(B) A-phase Chum Atg B
P Qpx Mn-Opx OrFsp(C1) AbFsp(C1) Pl(I1,HP)
Fsp(C1) MuPaMa(CH)
refer to the solution model glossary, or read the commentary within the solution model file itself, for more information about the solution models.
Bio(HP)
melt(HP)
Pheng(HP)
St(HP)
San
Pl(h)
Gt(HP)
The solution model file defines the following dependent endmembers:
mnts_i sdph_i fame_i fafchl_i mame_i mafchl_i fets_i
fsp4_i ftat_i hfcrd_i hmncrd_i fparg_i fts_i fgl_i
ncel_i nfcel_i
Exclude any of these endmembers (y/n)?
Answer no if you do not understand this prompt.n
Enter calculation title:
test 19
C\jamie\Berple_X> vertex
Enter computational option file name (i.e. the file created with BUILD), left justified:
in19.dat
Reading thermodynamic data from file: hp02ver.dat Writing print output to file: print19 Writing plot output to file: plot19 Writing pseudocompound glossary to file: pseudocompound_glossary.dat Reading solution models from file: solution_model.datWriting bulk composition plot output to file: bplot19
VERTEX creates an additional file named by adding a prefix "b" to the plot file name "plot19", this file, "bplot19", is needed by both PSVDRAW and WERAMI and should not be deleted or moved independently of the primary plot file. The polygon file mentioned below ("pplot19") is not used for this type of calculation.
Generating pseudocompounds, this may take a while...**warning ver114** the following endmembers are missing for Bio(HP)mnbi mnts_iEndmember configurational entropies (doc. eq. 8.2) for Bio(HP) are:ann - 11.52622 phl - 11.52622 east - 0.00000sdph_i - 0.00000**warning ver041** icky pseudocompound names for solution model: Bio(HP)refer to pseudocompound_glossary.dat file for pseudocompound definitions.1678 pseudocompounds generated for: Bio(HP)**warning ver041** icky pseudocompound names for solution model: melt(HP)refer to pseudocompound_glossary.dat file for pseudocompound definitions.84483 pseudocompounds generated for: melt(HP)
Because of the large number of pseudocompounds generated for the melt phase this calculation may require the "large parameter" version of VERTEX.
... output abridged ...
Done generating pseudocompounds (total: 100489)
1.3% done with low level grid.
3.8% done with low level grid.
... output abridged ...
94.9% done with low level grid.
97.5% done with low level grid.
100.0% done with low level grid.
Beginning grid refinement stage.324 grid cells to be refined at grid level 2...working (501 minimizations done)refinement at level 2 involved 688 minimizations2288 minimizations required of the theoretical limit of 6400
C\jamie\Berple_X> psvdraw
Enter the Perple_X plot file name:plot19
PostScript will be written to file: plot19.ps
PSVDRAW converts the numeric data in plot19 to PostScript graphics in the file plot19.ps; this file can be viewed in standard PostScript viewers (e.g., GhostView) or edited in most modern graphical editors (e.g., CorelDraw or Illustrator).
Modify the default plot (y/n)?
n
The postscript output is plotted below (Figure 2).
Figure 2. Computed phase relations as output by PSVDRAW, this figure differs from Figure 1 partially because of low compositional resolution and the coarseness of the grid, but primarily because the high resolution model for the melt was simplified by excluding the anL, fo8L, fa8L, and sil8L endmembers. These endmembers were excluded after an analysis similar to that reproduced in the next section showed they were present in minor quantities. The most significant effect of the simplification is that the high temperature field sil+Gt+Pl+San+melt expands to higher water contents because of the absence of a calcium component in the melt.
Once a pseudosection has been calculated with VERTEX the program WERAMI can be used to recover information from the output. Calculations by gridded minimization in VERTEX, such as the present example (Figure 2), have two sources of discretization error (roughness): error associated with mapping on a grid, which may be reduced by refining the grid parameters; and error resulting from the finite spacing of the pseudocompounds used to represent that stable phases. The latter type of error is particularly important for complex solution phases such as a silicate melt, since the number of pseudocompounds necessary to resolve the composition accurately over the entire range of compositions possible may be astronomically large. A simple strategy to overcome this problem is to make an initial low resolution calculation and use the results to restrict the compositional range and refine the resolution of the solution model. For the present calculation the initial compositional range for the melt was specified by the following lines of the solution model "melt(HP)" in the solution model file "solution_model.dat":
0.0 0.75 0.03 | range and resolution of X(h2oL)
0.0 0.03 0.03 | range and resolution of X(fo8L)
0.0 0.03 0.03 | range and resolution of X(fa8:)
0.0 0.27 0.03 | range and resolution of X(abL)
0.0 0.06 0.03 | range and resolution of X(sil8L)
0.0 0.06 0.03 | range and resolution of X(anL)
0.0 0.30 0.03 | range and resolution of X(kspL)
where the first two numbers on each line give the minimum and maximum mole fraction of the endmember (indicated by the commentary on the right), and the third number gives the compositional resolution. Note that the fraction of the remaining endmember for this model (q8L) is not defined explicitly, but is determined by difference from the other endmembers. The compositions of the endmembers are:
h2oL = H2O
fo8L = Mg4Si2O8
fa8L = Fe4Si2O8
abL = NaAlSi3O8
sil8L = Al3.2Si1.6O8
anL = CaAl2Si2O8
kspL = KAlSi3O8
A simple means of establishing the range of melt compositions (in terms of these endmembers) is to sample the stable melt compositions computed by VERTEX on a regular grid using the program WERAMI.
To reiterate, we have two goals in performing such a test:
1) To be certain that the existing subdivision range is not too restrictive, i.e., that a solutions composition is not artificially limited by the minimum and maximum values specified for the model. E.g., in the melt model above h2oL has an upper limit of 0.75, if we see that this composition is stable it is probable that we have artificially limited the melt water content and we should expand the range of water compositions considered and repeat the calculation.
2) To refine the range of compositions considered so that we can increase the compositional resolution (i.e., accuracy) of the model in question in subsequent calculations.
The WERAMI dialog that accomplishes this for end-members sil8L, h2oL, and siL is reproduced below:
C\jamie\Berple_X> werami
Enter the VERTEX plot file name:
plot19
Select operational mode:
1 - compute properties at specified conditions2 - create a property grid (plot with pscontor)3 - compute properties along a curve or line (plot with pspts)4 - as in 3, but input from file 2Select a property:
1 - Specific Enthalpy (J/m3)
2 - Density (kg/m3)
3 - Specific heat capacity (J/K/m3)
4 - Expansivity (1/K, for volume)
5 - Compressibility (1/bar, for volume)
6 - Weight percent of a component
7 - Mode (Vol %) of a compound or solution
8 - Composition of a solution
9 - Grueneisen thermal ratio
10 - Adiabatic bulk modulus
11 - Shear modulus (bar)
12 - Sound velocity (km/s)
13 - P-wave velocity (Vp, km/s)
14 - S-wave velocity (Vs, km/s)
15 - Vp/Vs
16 - Specific Entropy (J/K/m3)
17 - Entropy (J/K/kg)
18 - Enthalpy (J/kg)
19 - Heat Capacity (J/K/kg)
20 - Specific mass of a phase (kg/m3-solid)
8
Enter solution or compound name (left justified):
melt(HP)
Compositions are defined as a ratio of the form:
Sum {w(i)*n(i), i = 1, c1} / Sum {w(i)*n(i), i = c2, c3}n(j) = number of moles of component jw(j) = weighting factor of component j (usually 1)
The sole complication in this problem is that we want to know the melt composition in terms of the model endmembers, but WERAMI defines compositions in terms of the systems components (usually oxides). The algebra is simple, but to provide an example we are interested in the mole fraction (or, in this case, equivalently number of moles) of the sil8L endmember. To relate this to number of moles of the system component Al2O3 we may write:
nAl2O3 = 8/5 nsil8L + 1/2 nabL + 1/2 nkfsL + nanL
then we have
nabL = 2 nNa2O
nkfsL = 2 nK2O
nanL = nCaO
and substituting these into the expression for nAl2O3 and rearranging we obtain
nsil8L = 0.625 nAl2O3 - 0.625 nNa2O - 0.625 nK2O - 0.625 nCaO
which is the equation for the composition of interest. In WERAMI such a composition can be created by specifying it as the "numerator" of a composition as done in response to the following prompts
How many components in the numerator of the composition?
4
Component indices and weighting factors for the
compositions numerator?
1 - H2O
2 - FEO
3 - MGO
4 - CAO
5 - K2O
6 - NA2O
7 - AL2O3
8 - SIO2
7 0.625 6 -0.625 5 -0.625 4 -0.625
How many components in the denominator of the composition? Enter zero to plot the numerator.
0
The compositional variable is: 0.6 AL2O3
The compositional variable is: -0.6 NA2O
The compositional variable is: -0.6 K2O
The compositional variable is: -0.6 CAO
The above output is unfortunate, but correct (some day I'll get around to fixing it).
Happy (y/n?)
y
Change default variable range (y/n)?
n
Enter number of nodes in the x and y directions: (help)
100 100
Writing grid data to file: cplot19
Range of >0 data is: 0.248365E-09 -> 0.300000E-01
The file cplot19 can be plotted with the Perple_X program PSCONTOR, or in MatLab with the Perple_X Matlab script "surface_plot". In any case, the range reported above is the range of nsil8L for the calculation. Based on this result the line in the melt(HP) model:
0.0 0.06 0.03 | range and resolution of X(sil8L)
could be replaced with something like
0.0 0.045 0.015 | range and resolution of X(sil8L)
here the upper limit is not set to the upper end of the observed range because compositions are uncertain by roughly half the compositional resolution.
Evaluate additional properties (y/n)?
y
Select a property:
1 - Specific Enthalpy (J/m3)
2 - Density (kg/m3)
3 - Specific heat capacity (J/K/m3)
4 - Expansivity (1/K, for volume)
5 - Compressibility (1/bar, for volume)
6 - Weight percent of a component
7 - Mode (Vol %) of a compound or solution
8 - Composition of a solution
... output abridged ...
20 - Specific mass of a phase (kg/m3-solid)
8
Enter solution or compound name (left justified):
melt(HP)
Compositions are defined as a ratio of the form:
Sum {w(i)*n(i), i = 1, c1} / Sum {w(i)*n(i), i = c2, c3}n(j) = number of moles of component jw(j) = weighting factor of component j (usually 1)How many components in the numerator of the composition?
1
Component indices and weighting factors for the
compositions numerator?
1 - H2O
2 - FEO
3 - MGO
4 - CAO
5 - K2O
6 - NA2O
7 - AL2O3
8 - SIO2
1 1
How many components in the denominator of the composition? Enter zero to plot the numerator.
0
The compositional variable is: 1.0 H2O
Happy (y/n?)
y
Writing grid data to file: ccplot19
Range of >0 data is: 0.450000 -> 0.690000
Given that the melt field extends to X(H2O) = 0, it may seem peculiar that the water content of the melt does not go to zero. The explanation for this is that the amount of melt goes to zero at X(H2O) = 0, but at the smallest non-zero value of X(H2O) the amount of water in the melt is 0.45. Thus we can replace the line in the melt(HP) model:
0.0 0.75 0.03 | range and resolution of X(h2oL)
with something like:
0.435 0.705 0.015 | range and resolution of X(h2oL)
and as a final example consider nabL (= 2 nNa2O):
Evaluate additional properties (y/n)?
y
Select a property:
1 - Specific Enthalpy (J/m3)
2 - Density (kg/m3)
3 - Specific heat capacity (J/K/m3)
4 - Expansivity (1/K, for volume)
5 - Compressibility (1/bar, for volume)
6 - Weight percent of a component
7 - Mode (Vol %) of a compound or solution
8 - Composition of a solution
... output abridged ...
20 - Specific mass of a phase (kg/m3-solid)
8
Enter solution or compound name (left justified):
melt(HP)
Compositions are defined as a ratio of the form:
Sum {w(i)*n(i), i = 1, c1} / Sum {w(i)*n(i), i = c2, c3}n(j) = number of moles of component jw(j) = weighting factor of component j (usually 1)How many components in the numerator of the composition?
1
Component indices and weighting factors for the compositions numerator?
1 - H2O
2 - FEO
3 - MGO
4 - CAO
5 - K2O
6 - NA2O
7 - AL2O3
8 - SIO2
6 2
How many components in the denominator of the composition? Enter zero to plot the numerator.
0
The compositional variable is: 2.0 NA2O
Happy (y/n?)
y
Writing grid data to file: cccplot19
Range of >0 data is: 0.862049E-01 -> 0.180000
Thus we can replace the line in the melt(HP) model:
0.0 0.27 0.03 | range and resolution of X(abL)
with something like:
0.075 0.195 0.015 | range and resolution of X(abL)
In principle, this procedure should be repeated for every endmember that has a restricted compositional range in every solution that is stable in the calculated section. By imposing such restrictions it is possible to resolve solution compositions with high accuracy (e.g., 0.01 mol%).