Introduction

The Perple_X programs BUILD, VERTEX, FRENDLY, MEEMUM, WERAMI and PSSECT look for an option file that contains keywords that control computational behavior. This option file is specified in the problem definition file generated by BUILD and defaults to perplex_option.dat. If no option file is found, then Perple_X uses the default values for each option. This page documents these options. The actual values for all relevant options are output to the user console when a program is run. Perple_X solution model and thermodynamic data files (e.g., solution_model.dat) may also contain optional keywords that control how data is treated. Some of these keywords are documented here.

Entries in the option file take the general form

keyword value1 value2 .... | commentary

where the keyword identifies an option and the associated values (e.g., on, off or a number) characterize the option. Comments may be placed anywhere in the file provided they are preceded by a "|" character. In Perple_X 6.8.1+, any keyword may be assigned the value "default", in which case the keyword is assigned its default attributes.

BEST PRACTICE: to avoid confusion, create personalized and/or problem specific option files (e.g., my_problem_option.dat) that list only those options that have non-default values.

NOTE: Perple_X PostScript plotting programs (e.g., PSSECT, PSVDRAW, PSPTS, PSTABLE) read an additional option file. The second option file, named perplex_plot_option.dat, specifies plot options, see Perple_X plot options for details.

6.9.1+ optimization option group

The 6.9.1 version of Perple_X uses an iterative strategy in which the continuous composition space of a solution phase is initially represented by a static set of discrete compositions, i.e., pseudocompounds. Stable and nearly stable compositions, i.e., refinement points, are identified from this representation by linear programming (LP). The composition space about the refinement points is then resampled and the LP optimization repeated until a specified precision has been achieved. The resampling between LP optimizations is done by quadratic programming (QP), which optimizes the composition of each refinement point relative to the current LP solution. Phase diagram sections are calculated by the program vertex in two stages: an exploratory stage and an auto-refine stage. During the exploratory stage a low resolution set of static compositions is used to determine the approximate range of the stable phase compositions in the section. The compositions determined in this manner form the set of static compositions considered during the auto-refine stage. The details of this algorithm and various thresholds are controlled by options that are documented here collectively. Tuning with these options can be frustrating because they are not independent and changing them may have non-intuitive consequences. 

Useful options:

NOTE: setting intermediate_savrpc and intermediate_savdyn to T is the most general method of remedying computational problems in vertex and meemum. When this method fails systematically explore the effect of the options listed below. It is often helpful to use meemum with the output_iteration_details and output_iteration_G set to T in order to understand these effects.

• optimization_precision - specifies the difference in Gibbs energy during successive LP optimizations at which the optimization is considered to have converged; default: 1e-4 J/mol; practical range: [1e2, 1e-6]. Small values increase computational cost and may lead to failed optimizations (marked by red patches in phase diagram sections); excessively large values cause rough phase boundaries.

• replicate_threshold - during the exploratory stage of a calculation in vertex: a stable, or nearly stable, composition is added to the list of static compositions to be considered during the auto-refine stage of the calculation if it is separated from all compositions in the list by a Euclidean distance greater than the replicate_threshold value; default: 1e-3 mol; practical range: [1e-2, 1e-8]. replicate_threshold effectively defines the resolution of the static compositional array used during the auto-refine stage. Small values increase computational cost and may lead to failed optimizations (marked by red patches in phase diagram sections); excessively large values cause rough phase boundaries.

• rep_dynamic_threshold - during QP in vertex/meemum: if a dynamically-generated composition is separated from a previous dynamically-generated composition by a Euclidean distance smaller than the replicate_threshold value, then the composition is not added to the list of compositions considered during subsequent LP optimizations; default: 1e-3 mol; practical range: [1e-2, 1e-6]. Small values increase computational cost and may lead to failed optimizations (marked by red patches in phase diagram sections); excessively large values cause rough phase boundaries.

• intermediate_savrpc - in vertex/meemum: controls whether compositions are added to the list of dynamically generated compositions during intermediate stages of QP optimization; default: F (false). Setting intermediate_savrpc to T (true) increases computational cost and may increase optimization precision.

• intermediate_savdyn - during the exploratory stage of a calculation in vertex: controls whether compositions from intermediate LP optimizations are added to the list of static compositions to be considered during the auto-refine stage of the calculation; default: F (false). Setting intermediate_savrpc to T (true) increases computational cost and may increase optimization precision.

Useless new options: these options control aspects of the 6.9.1+ algorithm, the default choices are likely optimal.

• optimization_max_it - if the number of iterations during successive LP exceeds optimization_max_it iteration is terminated regardless of whether the optimization_precision value has been achieved; default: 40.

• MINFRC_diff_increment - the increment used for evaluation of finite differences during QP when analytical derivatives are not available; default: 1e-7; practical range [1e-2, 1e-8].

• scatter-points - controls whether additional compositions are generated about a final QP result; default: T (true). Setting scatter_points to F (false) decreases computational cost.

• scatter-increment - the compositional increment used to generate the compositions requested if the scatter-points option is T; default 1e-2 mol; practical range [1e-2, 1d-7].

• keep_all_rpcs - controls whether the list of dynamic compositions is reset after each LP optimization within a successive series; default: T (true). Setting keep_all_rpcs to F (false) decreases computational cost and optimization precision.

• re-refine - causes the auto-refine data file to be updated during the auto-refine stage of a calculation in vertex; default: F (false). The updated auto-refine data can be used in repeated auto-refine stage calculations if the auto_refine keyword has been set to manual.

Some observations re tuning relative to the default values of the above options:

• Setting intermediate_savdyn to T, followed by setting intermediate_savrpc to T, are the changes most likely to remedy rough phase boundaries.

• Sequentially increasing the values of the optimiziation_precision, rep_dynamic_threshold, and replicate_threshold are the changes most likely to remedy sections with irregular red patches indicative of failed optimizations; if these values excessive, then computed phase boundaries will roughen.

• Setting intermediate_savdyn to T is the change most likely remedy smooth red patches that may appear in sections computed with lagged aqueous speciation .

abbreviation

NOTE: abbreviation is a not a perplex_option file keyword, the abbreviation keyword is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the keyword and its value on a line after the solution model name.

The abbreviation keyword specifies the abbreviation used by Perple_X on output if solution_names is set to abb[reviation]. The abbreviation must be < 7 characters, it need not be unique to the solution model.

This keyword is only relevant for WERAMI, PSSECT, and MEEMUM.

Other keywords relevant to solution model names: solution_names, full_name.

absolute

The absolute keyword controls whether WERAMI (computational modes 2-4) outputs relative or absolute molar/mass compositions. Whether WERAMI outputs molar or mass quantities is determined by the composition_phase and composition_system keywords.

This keyword may take values: T (true) or F (false). The default is F.

Anderson-Gruneisen

The Anderson-Gruneisen keyword controls the parameterization of high pressure polythermal equations of state (Murnaghan, Birch-Murnaghan).

This keyword may take values: T (true) or F (false). The default is T.

If the keyword is T [true], then the temperature derivative of the bulk modulus is computed as a function of the pressure derivative of the bulk modulus and the expansivity at the reference pressure as described by Helffrich & Connolly (2009). If the keyword is F, then the temperature derivative of the bulk modulus is assumed to be an independent model parameter.

The utility of this option it corrects a tendency of certain thermodynamic formulations (notably Holland & Powell 1998) to generate unrealistic physical properties. This correction is particularly important for seismic velocity calculations, but has the unfortunate consequence that it may influence calculated phase equilibria. A means of implementing this correction for purposes of seismic velocity calculations without affecting computed phase relations is to set Anderson-Gruneisen to F for the calculation of phase equilibria in VERTEX and subsequently set Anderson-Gruneisen to T for the calculation of seismic velocities with WERAMI. This method is not thermodynamically consistent, but the inconsistency is unlikely to be of significance.

Other keywords relevant to seismic velocity calculations: vrh/hs_weighting, bounds, explicit_bulk_modulus, poisson_ratio, melt_is_fluid, interpolation, seismic_output, seimsic_data_file.

approx_alpha

The approx_alpha keyword controls whether the approximation exp(x)-> 1+x is used to evaluate volume at the reference pressure for phases described by EoS choices (1-4).

This keyword may take values: T (true) or F (false). The default is T.

If the keyword is T [true], then the approximation

            V(T,P_r) ≈ V(T_r,P_r)·[1 + integral(α(T,P_r),T=Tr..T)]

is used, otherwise the exact form

            V(T,P_r) = V(T_r,P_r)·exp[integral(α(T,P_r),T=Tr..T)]

is used. Although the approximate form is inaccurate at high temperature it has been assumed during the derivation of certain data bases (most notably that of Holland & Powell 1998), therefore the approximation should be used with such data bases to ensure consistency.

aq_bad_results

The aq_bad_results keyword controls error handling during lagged aqueous speciation calculations, it may take the following values:

err - any suspect result is reported as a failed optimization.

101 - if a solute component is dissolved entirely in the solvent, cease iteration and output the result. The results satisfy mass and charge balance, but generally have not been refined to the target resolution (final_resolution) and may reflect the influence of numerical instability.

102 - do not allow extrapolation of HKF into vapor-like density field or coexistence of pure and impure solvent.

103 - implemented?

ign - output all results regardless of suspect behavior.

The default value is err for all computational modes other than 0-d phase fractionation. The default for 0-d phase fractionation is 101.

See also: aq_solvent_solvus

aq_ion_H+

The aq_ion_H+ keyword controls whether the hydronium ion is used as the reference electrolytic species (Eqs 3-8, Connolly & Galvez 2018) in lagged and simple back-calculated aqueous speciation calculations. The hydroxyl ion is used as the reference species if aq_ion_H+ is false.

This keyword may take values: T (true) or F (false). The default is T.

aq_lagged_iterations

In lagged aqueous speciation calculations, the chemical potentials from the previous iteration of an adaptive optimization are used to compute the speciation of electrolytic fluids. The aq_lagged_iterations keyword permits the user to require additional intermediate iterations so that the lagged chemical potentials converge on the current chemical potentials. The need for these iterations can be evaluated by comparing the lagged aqueous speciation with the back-calculated result (obtained if aq_output is true). If the lagged and back-calculated results differ, then specifying a small number of intermediate iterations will cause the results to converge. In general intermediate iterations are unnecessary because they do not improve numerical stability and because chemical potentials converge rapidly during adaptive optimization (the chemical potentials can be monitored by activating output_iteration_G)

The lagged_aq_iterations keyword takes an integer value, the default is 0.

See also: aq_output, aq_solvent_composition, aq_solute_composition, output_iteration_G, species_output

aq_lagged_speciation

The aq_lagged_speciation keyword controls whether lagged aqueous speciation calculations are done by WERAMI and MEEMUM. The speciation is output only if a recognized solvent phase is stable and data for aqueous species is present in the thermodynamic data file used for the calculation. 

This keyword may take values: T (true) or F (false). The default is T.

See also: aq_output, aq_solvent_composition, aq_solute_composition, output_iteration_G, species_output

aq_output

The aq_output keyword controls whether simple back-calculated aqueous speciation calculations are done by WERAMI and MEEMUM. The speciation is output only if a recognized solvent phase is stable and data for aqueous species is present in the thermodynamic data file used for the calculation. 

This keyword may take values: T (true) or F (false). The default is T.

See also: aq_species, aq_solvent_composition, aq_solute_composition, aq_lagged_speciation

aq_oxide_components

The aq_oxides keyword permits suppression of tests for chemical degeneracy during lagged- and back-calculated speciation calculations. These tests must be suppressed for such calculations if a thermodynamic data file specifying oxide components is used (this practice is NOT recommended).

This keyword may take values: T (true) or F (false). The default is F.

See also: aq_species, aq_solvent_composition, aq_solute_composition, aq_lagged_speciation

aq_species

The aq_species keyword controls the number of aqueous species, ranked by abundance, output for simple back-calculated aqueous speciation calculations done by MEEMUM and WERAMI (computational mode 1). All aqueous species are output, without ranking, in WERAMI mode 2-4 calculations. 

This keyword takes positive integer values. The default is 20.

aq_solute_composition

The aq_solute_composition keyword controls whether the concentrations of solute species in simple back-calculated aqueous speciation calculations are output in molal units (mole/kg-solvent) or as mole fractions.

This keyword may take values: m (molar) or y (mole fractions). The default is m.

aq_solvent_composition

The aq_solvent_composition keyword controls whether the concentrations of solvent species in simple back-calculated aqueous speciation calculations are output in molal units (mole/kg-solvent) or as mole fractions.

This keyword may take values: m (molar) or y (mole fractions). The default is y.

aq_solvent_solvus

The aq_solvent_solvus keyword (lopt(46)) controls whether solute-free solvent compositions are generated during lagged speciation calculations. This is necessary if a vapor-like phase may separate from a solute-bearing fluid during lagged speciation calculations. The current implementation of aq_bad_results may interfere in phase separation problems and should be checked.

This keyword may take values: T (true) or F (false). The default is F.

aq_vapor_epsilon

The aq_vapor_epsilon keyword sets a threshold for the solvent dielectic constant below which the solvent is considered to be vapor and incapable of dissolving solutes. The current implementation of aq_bad_results may interfere with the output of vapor-phase results and should be checked.

This keyword takes a real value. The default is unity.

auto_exclude

The auto_exclude keyword prevents the inclusion of thermodynamic phases and species (typically gas phase species) with no associated mechanical equation of state in Gibbs energy minimization calculations. For instructions on how to associate a molecular fluid EoS with gas species data see special_EoS.

This keyword may take values: T (true) or F (false). The default is F.

auto_refine

The auto_refine keyword controls whether Perple_X (specifically the programs VERTEX, MEEMUM, and CONVEX) uses results from an "exploratory" calculation to refine a subsequent recalculation of the same problem, i.e., an "auto-refined" calculation. The exploratory calculation is used to establish the stable solution compositions. This information is saved (even if auto_refine is off) in a file named by concatenating the project name with the "arf" file type suffix. For example, if the project is named in, VERTEX or CONVEX generates a file named in.arf and, if the option_list_files keyword is T, a more easily interpreted version named in_auto_refine.txt.

In the auto-refine stage of a calculation, VERTEX and CONVEX:

Eliminate solutions that were not stable in the exploratory calculation.

 

Restrict compositional ranges of solutions to the ranges established in the exploratory calculation.

 

Use the second, auto-reine, value of the initial_resolution and final_resolution keywords.

 

Change mapping parameters for gridded minimization and phase fractionation calculations or change variance and search increment specifications for Schreinemakers and mixed-variable diagram calculations.

MEEMUM does not generate auto_refine data, but if such data exists from a calculation with VERTEX or CONVEX, then MEEMUM prompts if the data should be used as above.

auto_refine may be off, man, or aut; the default is man. If auto_refine = man, VERTEX must be run independently for the exploratory and auto-refine stages of a calculation. This manual mode allows users to examine results from the exploratory stage before undertaking the more time intensive auto-refine stage. If auto_refine = aut, VERTEX automatically does both the exploratory and auto-refine stages in a single run.

auto_refine_file (modified 6.9.1)

The auto_refine_file controls whether the range of solution compositions discovered during the exploratory stage of a calculation are output to a text file. If auto_refine_file = T, then the file is output and named my_project_auto_refine.txt, where my_project is the project name.

This keyword may take values: T (true) or F (false). The default is F (prior to 6.9.1: T).

This keyword affects VERTEX and CONVEX.

bad_number

The bad_number keyword determines the value assigned to missing data or bad numerical results (usually caused by floating point errors). Depending on the physical property of interest it may be useful to change this value so that bad results can be distinguished during post-processing (e.g., if seismic velocities are of interest, assigning a negative bad_number allows identification of erroneous velocities).

As of Perple_X revision 6.6.5.9, bad_number may be set to NaN (not-a-number). The advantage of setting bad_number to NaN is that advanced plotting programs such as MatLab and, to a certain extent, PyWerami (i.e., in contour mode) treat NaNs correctly as missing data. For example, if phase composition is contoured as a function of pressure and temperature with bad_number set to NaN, then the data will be only contoured where the phase is stable. In contrast, if bad_number is set to zero, zeroes will be reported for the composition wherever the phase is not stable; the zero values (usually) imply a range of composition that is much greater than the true range and consequently the default contour interval chosen by a contouring program will not resolve the data well. The Perple_X contour plot program PSTABLE is not capable of treating missing data and replaces NaNs with zeroes; thus there is no advantage to setting bad_number to NaN unless the data is to be processed with MatLab or PyWerami.

This keyword takes numeric values or NaN (< 12 characters), NaN is the default value.

This keyword affects WERAMI, FRENDLY and VERTEX.

bounds

Because the time scale for seismic wave propagation is short compared to the time scales for thermal and chemical equilibration, the elastic moduli (i.e., adiabatic bulk and shear moduli) relevant for the calculation of seismic wave speeds are not identical to the isostatic (Reuss) limit assumed for thermodynamic calculations*. In the absence of detailed textural information, the moduli are estimated as the weighted average of upper and lower bounds on the moduli. Two methods for the estimation of these bounds are the Hashin-Shtrikman (HS) and Voigt-Reuss-Hill (VRH) methods (Berryman, AGU Handbook of Physical Constants, 1995). The value of the bounds keyword (HS or VRH) determines method is used. HS bounds are narrower than the VRH bounds and are theoretically justified; thus, they are to be preferred. Despite this advantage, the VRH bound is more widely used in geoscience, presumably because it is simpler to compute.

If bounds = VRH, the lower bound Z_- (i.e., Reuss limit) on the modulus Z of an aggregate is the harmonic mean of the corresponding moduli of its p constituent phases

Z_- = 1/[sum(x_i/Z_i,i=1..p)],       [1]

where x_i is the volume fraction of phase i; and the upper bound Z₊ (i.e., Voigt limit) is the arithmetic mean

Z₊ = sum(x_i*Z_i,i=1..p).       [2]

If bounds = HS, the lower and upper bounds Z_-/+ are

Z_-/+ = 1/[sum(x_i/[Z_i-Y_-/+],i=1..p)].       [3]

In Equation 3: for the adiabatic shear modulus μ

Y_-/+ = 4/3 μ_min/max,      [4]

where μ_min and μ_max are, respectively, the minimum and maximum shear moduli of the constituent phases; and for the adiabatic bulk modulus K

Y_-/+ = μ_min/max([9K_min/max+8μ_min/max]/[K_min/max+2μ_min/max])/6.       [5]

In Equations 3-5, the lower bound Z_- is computed with Y_-, K_min and μ_min; whereas the upper bound Z₊ is computed with Y₊, K_max and μ_max.

For either value of bounds, the aggregate modulus is

Z = (1-χ)*Z_- + χ*Z₊,      [6]

where the weighting factor χ is specified by the vrh/hs_weighting keyword.

By default bounds = VRH.

This option affects WERAMI, MEEMUM and FRENDLY. For calculations analyzed with WERAMI, changing this keyword does not necessitate repeating the primary calculation with VERTEX.

Other keywords relevant to seismic velocity calculations: vrh/hs_weighting, explicit_bulk_modulus, poisson_ratio, Anderson-Gruneisen, melt_is_fluid, interpolation, seismic_output.

*Prior to November 21, 2018; Perple_X computed the shear modulus of a solution as the molar-weighted mean of its endmember shear moduli, Weidner et al. (JGR, 1984) cite empirical evidence in support of this assumption and, in the absence of a non-isostatic EoS, there is no theoretical constraint on the relation between the shear moduli of a solution and its endmembers. However, discounting excess volume effects, the bulk modulus of a solution is given by the volume-weighted Harmonic (Reuss) average of the bulk moduli of its endmembers. Therefore, simplicity can be invoked as an argument to support the contention that the shear modulus of an impure phase should be estimated by the Reuss average as suggested by Stixrude & Lithgow-Bertelloni (GJI, 2005). In recognition of this argument the Reuss average has been employed in Perple_X for this purpose since November 21, 2018. Thus criticism voiced by Garber et al. (G3, 2019) about the use of the Voigt average in Perple_X is apt, but only relevant to earlier versions of Perple_X and Connolly & Kerrick (2002, and Connolly 2005). 

closed_c_space

The closed_c_space keyword controls whether compositional variables for gridded minimization calculations define a closed or open composition space. In gridded minimization calculations as a function of k compositional variables X(C₁)...X(C_k), the user specifies k+1 bulk compositions C₀...C_k, if closed_c_space = T, then the bulk composition of the system C is computed as

C = sum{X(C_i)*C_i, i=1...k} + C₀*[1-sum{X(C_i), i=1...k}],

whereas if closed_c_space = F, then

C = sum{X(C_i)*C_i, i=1...k} + C₀.

This keyword may take values: T (true) or F (false). The default is T.

This keyword is only affects VERTEX.

composition_constant

The composition_constant keyword controls whether the terms in user defined phase compositions may include a constant.

This keyword may take values: T (true) or F (false). The default is F.

This option only affects WERAMI.

See also: composition_phase, composition_system, proportions

composition_phase

The composition_phase keyword controls whether phase compositions are output in molar or mass units.

This keyword may take values: wt, mol. The default is mol.

This option only affects WERAMI.

See also: absolute, composition_constant, composition_system, proportions

composition_system

The composition_system keyword controls whether the amounts of a systems components are output in molar or mass units.

This keyword may take values: wt, mol. The default is wt.

This option only affects WERAMI.

See also: absolute, composition_constant, composition_phase, proportions

console_messages

The console_messages keyword controls whether messages to the user console are output (provided a print file is requested) during Schreinemakers and mixed variable diagram calculations.

This keyword may take values: on, off. The default is on.

This keyword affects VERTEX.

cumulative

The cumulative keyword controls whether WERAMI in computational mode 3 for property choice 36 (all system or phase properties) outputs the cumulative absolute composition of a phase or system. This option is only useful for computing the total mass or molar amount of components removed from a system by the fractionation of a phase. For this purpose, the absolute keyword must also be set to true. This keyword only affects WERAMI property choice 36 and will result in nonsensical results if used in WERAMI computational mode 2.

Whether WERAMI outputs molar or mass quantities is determined by the composition_phase and composition_system keywords.

This keyword may take values: T (true) or F (false). The default is F.

cumulative_modes

If the cumulative_modes keyword is set to on, then cumulative phase modes (by volume or weight as determined by the proportions keyword) are output if the "modes of all phases" property is selected in WERAMI. Given a list of phases, the cumulative mode of a phase is the mode of the phase plus the modes of all the phases that precede it in the list. This form of output is useful for constructing diagrams in which the variation in the proportions of the phases are plotted as a function of a third variable, e.g., pressure along a geotherm (see Example #24).

This keyword may take values: on, off. The default is off.

NOTE: As of 12/20/08 keyword is no longer read from the computational option file, rather it is set interactively if the "modes of all phases" property is selected in WERAMI.

See also: fancy_cumulative_modes

dependent_potentials

The dependent_potentials keyword controls whether dependent chemical potentials are output when chemographic data is output (provided a print file is requested) during non-adaptive minimization calculations. In adaptive minimization calculations the dependent potentials are output to  my_project.plt and can be analyzed with WERAMI.

WARNING: the VERTEX output file format depends on the dependent_potential keyword value, consequently output generated by the VERTEX with the keyword set to off cannot be read by WERAMI or PSSECT if the keyword is changed to on, and vice versa. There is no check for the consistency of the keyword value between programs, thus any inconsistency will cause a "hard" crash (I/O errors).

This keyword may take values: on, off. The default is off.

efficiency

The efficiency keyword specifies the level of redundant testing done during Schreinemakers diagram calculations.

This keyword takes integer values 1->5, the default is 3. High values increase computational efficiency, but also increase the probability that a [pseudo-]univariant curve may be skipped or incompletely traced.

This keyword affects VERTEX.

explicit_bulk_modulus

The adiabatic bulk modulus K_S(T,P) is an implicit function of the Gibbs energy used to compute phase equilibria (Equation 4 of Connolly & Kerrick 2002). By default, Perple_X exploits this dependence to compute K_S(T,P). This method has the virtue that the modulus is consistent with the equation of state used to compute phase relations. The importance of this consistency for seismic velocity calculations is debatable because phase relations depend directly on the Gibbs energy, whereas K_S(T,P) is dependent primarily on second order derivatives of the Gibbs energy. Thus, it can be argued that empirically calibrated expressions for K_S(T,P) are more accurate than the values obtained from an EoS intended only for phase equilibrium calculations (e.g., Holland & Powell 1998). To accommodate this case, the explicit_bulk_modulus keyword permits the use of empirical expressions for K_S(T,P).

If explicit_bulk_modulus = T (true), K_S(T,P) of any pure phase or endmember is computed from the expression

K_S(T,P) = k0 + k1·(T-T_r) + k2·(P-P_r)

provided that the parameters {k0, k1, k2} are specified for the phase in the thermodynamic data file. If explicit_bulk_modulus = T (true), K_S(T,P) for a solution phase is computed as the volumetrically weighted mean of the endmember properties provided the parameters {k0, k1, k2}. Under any other circumstances K_S(T,P) is computed by differentiation of the Gibbs energy function for the phase.

This keyword takes the character values T or F. The default value is F.

This option affects WERAMI, MEEMUM and FRENDLY. For calculations analyzed with WERAMI, changing this keyword does not necessitate repeating the primary calculation done by VERTEX.

Other keywords relevant to seismic velocity calculations: vrh/hs_weighting, bounds, poisson_ratio, Anderson-Gruneisen, melt_is_fluid, interpolation, seismic_output, seimsic_data_file.

extrapolation

The extrapolation keyword is only relevant for gridded minimization and has no effect unless interpolation (see below) is also on.

This keyword may take values: on, off. The default is on.

This option only affects WERAMI, extrapolation may cause floating point errors in Perple_X 07.

fancy_cumulative_modes

Cumulative modes generated by WERAMI in computational mode 3 for property choice 25 (modes of all phases) are, by default, ordered so that if a new phase appears along a path its cumulative mode corresponds to its real mode (i.e., the cumulative mode on the new phase initiates from zero). In contrast, if fancy_cumulative_modes is T and the appearance of a new phase is coincident with the disappearance of a phase, then the cumulative mode of the new phase is computed so that the new phase is located in the same relative position as the phase that disappeared. The rationale for this scheme is that the coincidence is only possible if the two phases are related by a univariant reaction. Finite resolution, i.e., internodal spacing, may have the consequence that more than one phase may appear or disappear between two adjacent nodes (i.e., the nodes may span multiple phase boundaries), in such cases the fancy_cumulative_modes option may lead to erratic results.

This keyword may take values: T (true) or F (false). The default is F.

fd_expansion_factor

The fd_expansion_factor keyword is the factor by which the finite difference increment used to compute high order derivatives increases with order. These derivatives are used in Perple_X to compute physical properties during post-processing. 

This keyword takes a real value. The default value is 2. 

If the first order finite difference increment for a variable is dv1, then the increment used to compute nth order finite difference increment dvn = dv1 * fd_expansion_factor^(n-1).  

See finite_difference_p for related information.

This keyword affects WERAMI, FRENDLY, and MEEMUM.

final_resolution (obsolete 6.9.1+)

The final_resolution keyword determines the (molar) precision with which phase compositions are calculated during adaptive minimization (Connolly 2009). Because resolution is discretized in Perple_X, the effective final resolution of adaptive minimization calculations is determined by finding the minimum number of iterations that yield precision below final_resolution. The effective final resolution is computed as outlined in the resolution factor keyword description. See Example 1 of the adaptive minimization keyword group discussion for additional information on the effect of this keyword. 

The final_resolution keyword takes two values between 0 and 1. The first value applies during the exploratory stage of auto-refine calculations and the second value applies in the final (auto-refine) stage of the calculation. If only one value is present it is applied for both stages, if the keyword is absent the default targets for the final resolution in the exploratory and auto-refine stages are 1e-2 and 1e-3 (mol), respectively. If final_resolution > initial_resolution, then there is no iterative refinement of phase compositions and the effective resolution is determined by the initial_resolution keyword.

The value of final_resolution does not affect memory consumption, but small values may significantly increase computational time. The minimum value of is limited by the conditions at which the requested resolution causes numerical instability (i.e., warning ver058, failed optimizations). These conditions depend on many factors, but, as a rule of thumb, on 32-bit machines final_resolution should not be << 10^-4 mol.

This keyword affects VERTEX and MEEMUM.

See also: resolution_factor, reach_increment, initial_resolution, output_iteration_G, adaptive minimization keyword group.

finite_difference_p

The finite_difference_p keyword controls the magnitude of the finite difference increment on pressure for first order derivatives. These derivatives are used in Perple_X to compute physical properties during post-processing. 

The keyword takes two real values, threshold and fraction. The default value for threshold is 10000 and that of fraction is 0.01. 

If the pressure for a calculation is greater than threshold then the pressure increment dp1 = pressure * fraction, otherwise the pressure increment is dp1 = threshold * fraction. 

See fd_expansion_factor for related information.

This keyword affects WERAMI, FRENDLY, and MEEMUM.

fractionation_hi_limit/fractionation_lo_limit

In phase fractionation calculations, the fractionation_hi_limit and fractionation_lo_limit keywords permit specification of fractionation thresholds such that: 1) the mass fraction of a phase must exceed the fractionation_hi_limit before it is fractionated; and 2) the residual mass fraction of the phase after fractionation is fractionation_lo_limit. If fractionation_hi_limit ≤ fractionation_lo_limit, then VERTEX emulates Rayleigh fractionation, i.e., any fractionated phase is removed if its amount exceeds zero leaving no residual.

Each keyword takes real values ≤ 1. The default for both keywords is zero. 

full_name

NOTE: full_name is a not a perplex_option file keyword, the full_name keyword is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the full_name keyword and its value on a line after the solution model name.

The full_name keyword specifies the full name used by Perple_X on output if solution_names is set to ful[l]. The full_name must be < 23 characters, it need not be unique to the solution model. The full_name tag is also used by BUILD to group solution models, e.g., to have BUILD group all orthopyroxene models together after the solution model prompt, all orthopyroxene models should be given the same full_name, e.g., 'orthopyroxene'.

This keyword affects BUILD, WERAMI, PSSECT, and MEEMUM.

Other keywords relevant to solution model names: solution_names, abbreviation.

global_reach_increment (obsolete 6.9.1+)

The global_reach_increment specifies an incremental increase in the range over which the compositional variables of solutions are allowed to vary between successive iterations during adaptive minimization. 

Experience suggests that except for immiscible solution models there is no benefit to increasing this range beyond the default (see resolution_factor, eq [1]) and because such an increase is costly in terms of memory, it is preferable to apply such increases only for specific solution models via the solution model file reach_increment keyword. If global_reach_increment > reach_increment, its value overrides reach_increment, otherwise the value of reach_increment is retained. 

See reach_increment for further details.

This keyword affects VERTEX and MEEMUM.

See also: final_resolution, reach_increment, initial_resolution, solvus_tolerance, adaptive minimization keyword group.

grid parameters (modified 6.9.1)

For gridded minimization VERTEX uses a multilevel grid refinement strategy in which phase relations are mapped on an initial grid of resolution x_nodes * y_nodes. This grid is refined grid_levels - 1 times by bisection (Connolly 2005). The x_nodes, y_nodes, grid_levels parameters are set by keywords of the same name. Each keyword takes two integer values. The first value is used for the exploratory stage of gridded minimization calculations, while the second value is used for the auto-refine stage. The effective resolution of a multilevel grid is equivalent to a single grid with (x_nodes - 1) * 2**(grid_levels - 1) + 1 in the x-direction and (y_nodes - 1) * 2**(grid_levels - 1) + 1 nodes in the y-direction.

The danger of using low values for x_nodes and y_nodes and a high number of grid_levels is that a small phase field that protrudes into a larger phase field will not be identified if the protrusion occurs between two nodes of the low resolution grid at which the larger field is stable. There is no simple rule for the best choices for x_nodes or y_nodes as they depend on the scale of the diagram and the heterogeneity of its phase fields, the default values are 10 (prior to 6.9.1: 40) and 40 for exploratory and auto-refinement stages of a calculation. The default values of grid_levels are 1 and 4 for exploratory and auto-refinement stages.

y_nodes is used for 1-d gridded minimization calculations.

For 1-d phase fractionation calculations the 1d_path keyword indicates the number of nodes taken to define the path in the exploratory and auto-refine stages of the calculation. The default values for 1d_path are 40 and 150 for the exploratory and auto-refinement stages of a phase fractionation calculation. As a rule of thumb, the latter value should be chosen such that the results do not change significantly if it is varied by a factor of two.

This keyword affects VERTEX.

hard_limits (obsolete 6.9.1+)

If the hard_limits keyword is set to off, then unnatural composition limits (i.e., X < 1 or X > 0) specified in the solution model file (e.g., solut_07.dat) may be relaxed during adaptive minimization calculations. This behavior permits users to specify restricted compositional ranges for complex (costly) models, yet allows VERTEX to learn new limits in the course of a calculation. hard_limits should be set to on if a solution model is duplicated in the solution model file in order to represent distinct compositional ranges of the solution. For example, if a model for Na-K mica is duplicated to distinguish Na- and K-rich micas. In this case it is conceivable that if calculations were done under conditions where the mica is fully miscible, VERTEX might expand the composition limit of Na-rich mica into the range of K-rich mica, or vice versa, resulting in confusing output.

This keyword may take values: on, off. The default is off.

This keyword affects VERTEX and MEEMUM.

hybrid_EoS

The hybrid_EoS_XXX keyword, where XXX may be H2O, CO2, or CH4, determines the internal molecular fluid equation of state to be associated with a pure XXX species fluid. The keyword may take integer values:

   0 - MRK, Modified Redlich-Kwong EoS, DeSantis et al. 1974

   1 - HSMRK, Kerrick & Jacobs 1981, invalid at P > ~4 GPa and at ambient conditions.

   2 - CORK, Holland & Powell 1998, valid only for H2O and CO2, invalid at ambient conditions.

   3 - BRMRK, Bottinga & Richet 1981, valid only for CO2

   4 - PSEoS, PSEoS Pitzer & Sterner 1994, valid only for H2O and CO2, invalid at ambient conditions.

   5 - Steam Table EoS, Haar et al 1982, valid only for H2O

   6 - Zhang & Duan 2005, valid only for water, invalid at T < ~700 K.

   7 - Zhang & Duan 2009, invalid, at least for H2O, at T < ~700 K; may be preferable to the MRK (current default) for CH4.

The default values for hybrid_EoS_H2O, hybrid_EoS_CO2, and hybrid_EoS_CH4 are 4, 4, and 0, respectively. 

increment

The increment keyword specifies the default search/trace variable increments for Schreinemakers and mixed-variable diagram calculations. Two values are specified, these are applied, respectively, for the exploratory and autorefine stages of calculation. The values of increment are relative, absolute increments are computed by mutliplying the increment value by the variable range.

This keyword affects VERTEX.

initial_resolution (modified 6.9.1+)

VERTEX and MEEMUM, 6.9.1+: 

VERTEX and MEEMUM read only one value for the initial_resolution keyword (if two values are present, the first value is applied). This value determines the default (molar) compositional resolution used for solution models in the exploratory stage of calculations with VERTEX. The value is also used in MEEMUM in calculations that do not use auto-refine data from a previous calculation with VERTEX. If initial_resolution is greater than zero, its value over-rides the resolutions specified for individual phases in the solution model file. 

initial_resolution takes a value between 0 and 1 and may be specified either as an integer fraction (e.g., 1/2) or real number. If initial_resolution is zero, then Perple_X will use the resolutions specified in the solution model file. Optimally, initial_resolution should be specified as an integer fraction of 1, other choices lead to asymmetric resolution with a widow composition near one that can be costly in calculations involving complex solution models. Experience suggests that a value of 1/4 is adequate for most calculations.

CONVEX and 6.9.0-:

The initial_resolution keyword takes two values that determine the default (molar) compositional resolution used for solution models in the exploratory and auto-refine stages of calculations with VERTEX, CONVEX, and MEEMUM. If initial_resolution is greater than zero, its value over-rides the resolutions specified for individual phases in the solution model file. For the adaptive minimization calculations (MEEMUM and VERTEX) the effective initial resolution (d0) is the appropriate, i.e., exploratory or auto-refine stage, value of initial_resolution and the final precision is specified by the final_resolution keyword. For unconstrained minimization calculations (CONVEX), initial_resolution specifies the effective compositional resolution.

In adaptive minimization calculations, the initial_resolution keyword controls the amount of memory allocated to static pseudo-compounds. Small initial_resolution values improves accuracy, but are costly in terms of both memory and computer time. The diagnostic **error ver041** in calculations with VERTEX, CONVEX, and MEEMUM indicates that initial_resolution is too small.  

This keyword takes two values between 0 and 1 and that may be specified as integer fractions (e.g., 1/16) or real number. If initial_resolution is zero, then Perple_X will use the resolutions specified in the solution model file. Optimally, initial_resolution should be specified as an integer fraction of 1, other choices lead to asymmetric resolution with a widow composition near one that can be costly in calculations involving complex solution models. Experience suggests that the optimal values for initial_resolution 1/16 and 1/48 for most calculations and for composition diagram calculations in CONVEX 1/16 and 1/160 (or less).

This keyword affects VERTEX, CONVEX, and MEEMUM.

interim_results

The interim_results keyword controls whether interim results are output by VERTEX during 2-dimensional multilevel gridded-minimization calculations. During each successive level roughly doubles the required computational time. Setting interim_results to auto or manual causes VERTEX to output data which can be plotted or analyzed with PSSECT and WERAMI before VERTEX has completed a calculation. This option allows the user to identify computational problems before the final result has been generated.

This keyword may take values: off, auto, manual. The default is auto.

If interim_results is set to auto, then PSSECT/WERAMI automatically select the latest interim result for analysis and VERTEX automatically deletes all interim results upon completing a calculation. 

If interim_results is set to manual, then PSSECT/WERAMI allow the user to select from among interim results generated by VERTEX and VERTEX does not delete the interim results upon completing a calculation.

If interim_results is set to off, then no interim results are output by VERTEX.

This keyword affects VERTEX, WERAMI, and PSSECT.

interpolation

The interpolation keyword is only relevant for gridded minimization and is currently only used for mode 2 calculations (sampling on a grid) in WERAMI.

WARNING: turning interpolation "on" slows data processing.

The interpolation keyword takes 2 values, value1 and value2

value1 is on or off, the default is on

value2 is an integer, the default is 2

When value1 is on WERAMI computes physical properties by interpolation/extrapolation of the properties of an assemblage at a sampling point by linear interpolation and/or extrapolation from the 3 closest grid nodes of the computational grid at which this assemblage is known to be stable. For this purpose WERAMI uses an algorithm that tries to locate 3 nodes bounding the sampling point, when this not possible extrapolation is used if the extrapolation keyword value is on. Figure 1 illustrates some consequences of interpolation and/or extrapolation. The primary danger of interpolation as currently implemented (i.e., this will change) is that it may homogenize nodes that represent 2 or more compositions of a phase separated by a solvus.

Value2 specifies the the range of nodes around the sampling point searched with the triangulation algorithm. For a multilevel grid with JLEV levels, the number of nodes on around the sampling point is value2*(2**(JLEV-1)). Figure 2 illustrates the effect of increasing value2, value2 = 0 is equivalent to turning interpolation off, small values increase the probability that WERAMI cannot find bounding interpolation points (in which case no interpolation done around the sample point), whereas large values reduce the accuracy of linear interpolation.

Figure 1. Water content of mineral+melt (i.e., excluding free water) assemblages for a calculation as a function of temperature (T) and the compositional variable X(C2) which represents the bulk water content of the system (from 0 to 5 wt%). The calculation was done on a low resolution (single level 20x20) grid, for plotting purposes this grid was sampled on a 50x50 grid with WERAMI. At high temperature all H2O component is dissolved in the melt phase and therefore the water content of the mineral+melt assemblage should vary linearly from 0 to 5 wt % as a function of X(C2), this is not the case if interpolation is turned off (first plot, "interpolation off") because the water content of the system is identified with discrete nodes of the grid. The advantage of viewing the data with interpolation off is that it provides an unambiguous picture of the raw data. Continued...

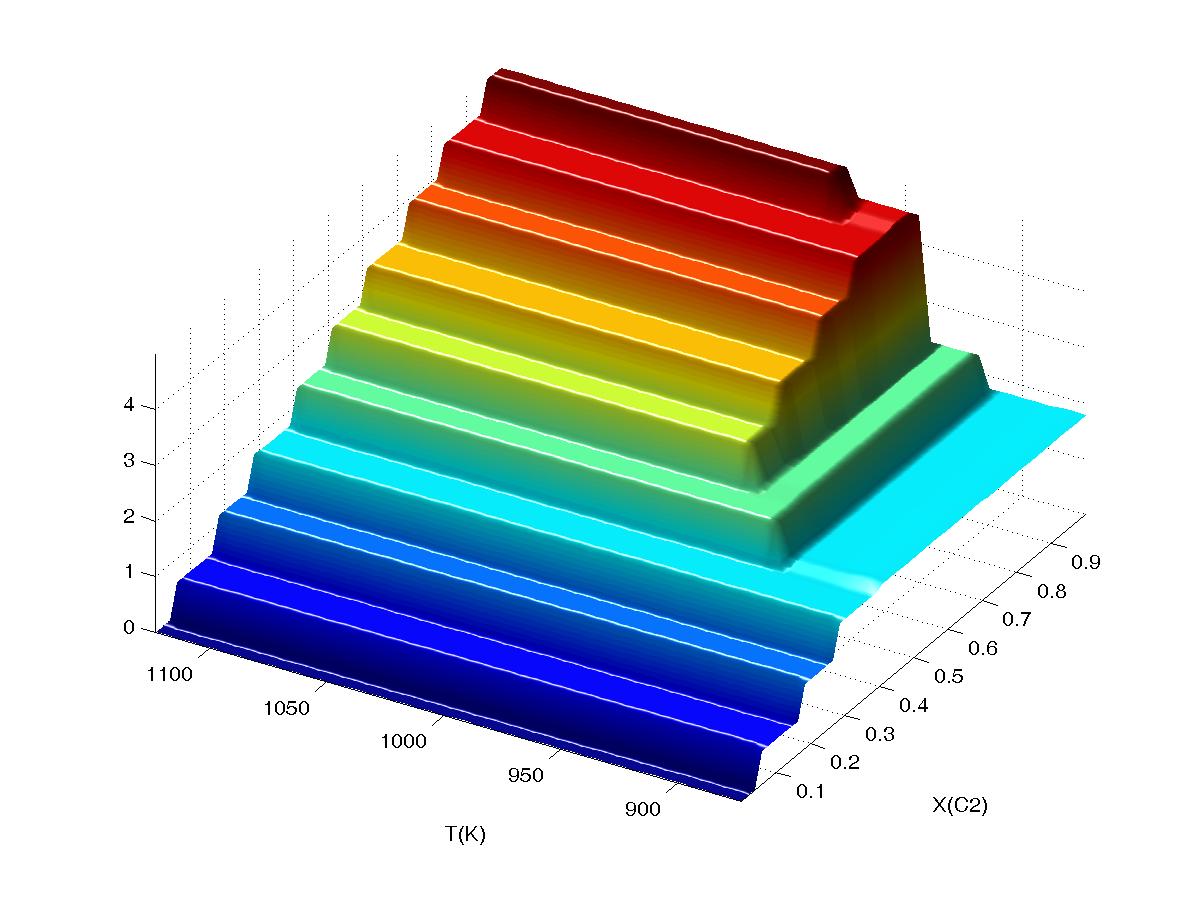
If interpolation is turned on, and extrapolation turned off (second plot, "interpolation on 2" and "extrapolation off"), the plot is smoothed, but discontinuities persist where WERAMI was unable to obtain identify three grid points representing the phase assemblage bounding the sampling points. Continued...

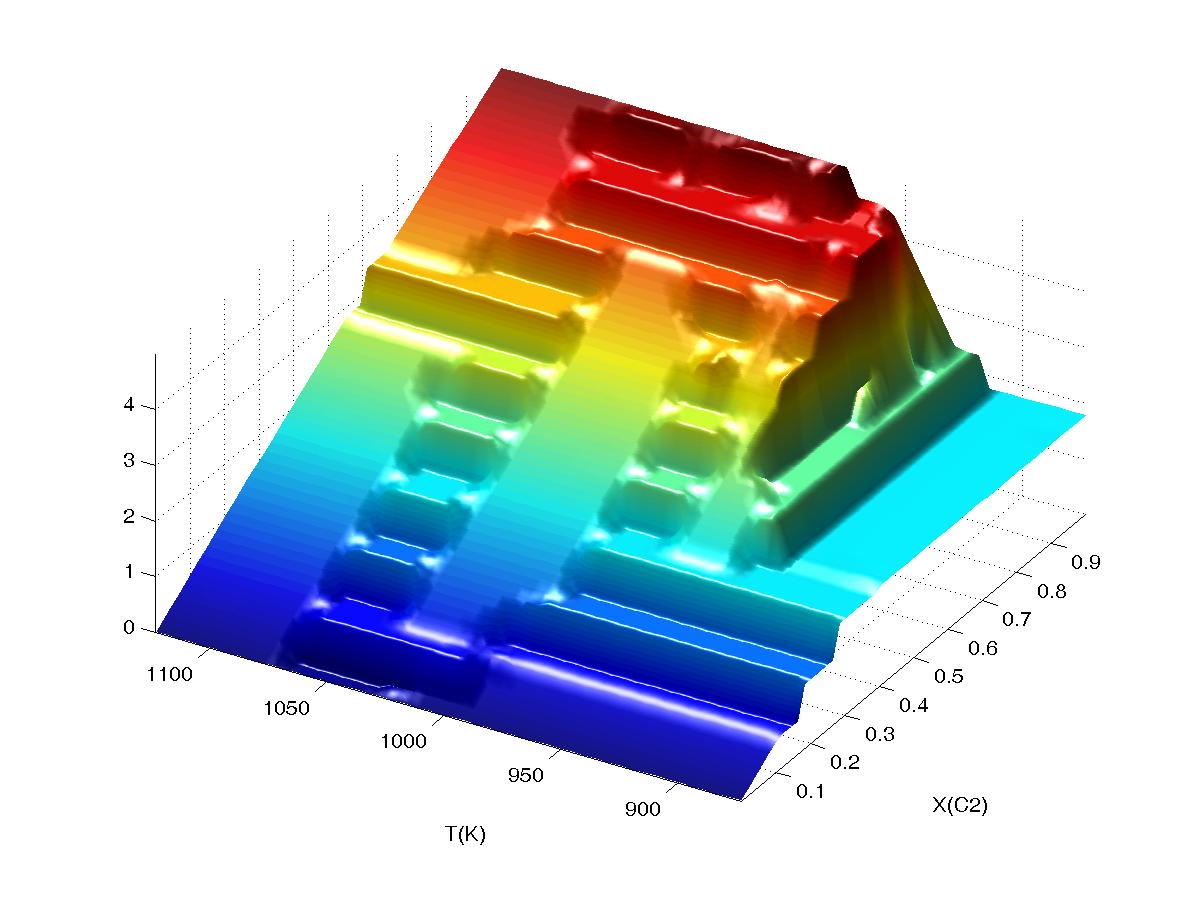
If both interpolation and extrapolation are on (third plot, "interpolation on 2" and "extrapolation on") the required smooth variation in water content at low temperature is obtained, although artificial plateaus persist where a particular phase assemblage is stable only at one node (e.g. at T~1050 K, X(C2)~0.6) or along a one-dimensional path (e.g., T<950 K, X(C2)~0.2). A disadvantage of allowing extrapolation, particularly in the case of sections with compositional variables, is that physically unrealistic values can be obtained, as at T~950 K, X(C2)~1 where the water content depicted is greater than the maximum possible for the system. The undesirable artifacts of extrapolation and interpolation depicted here become less significant and less frequent as resolution of the grid is increased.

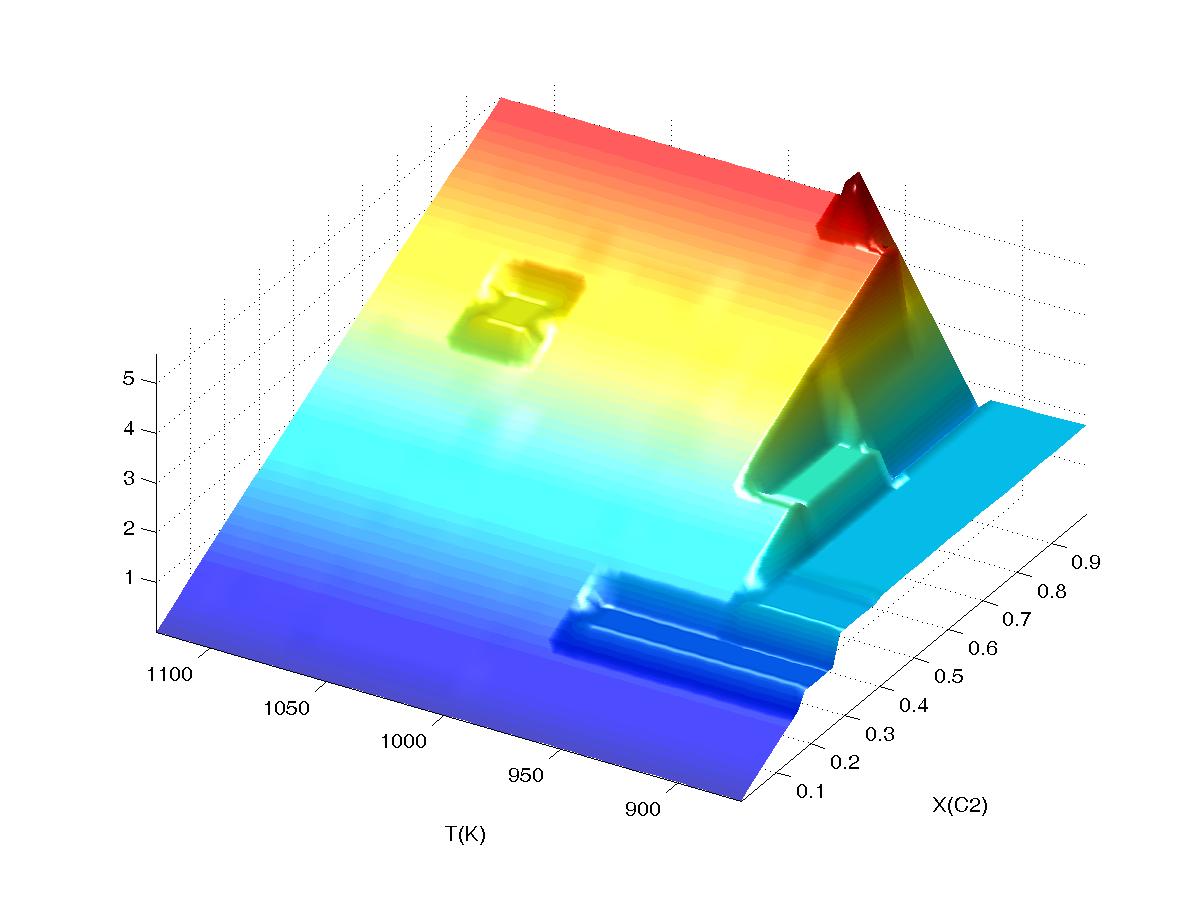
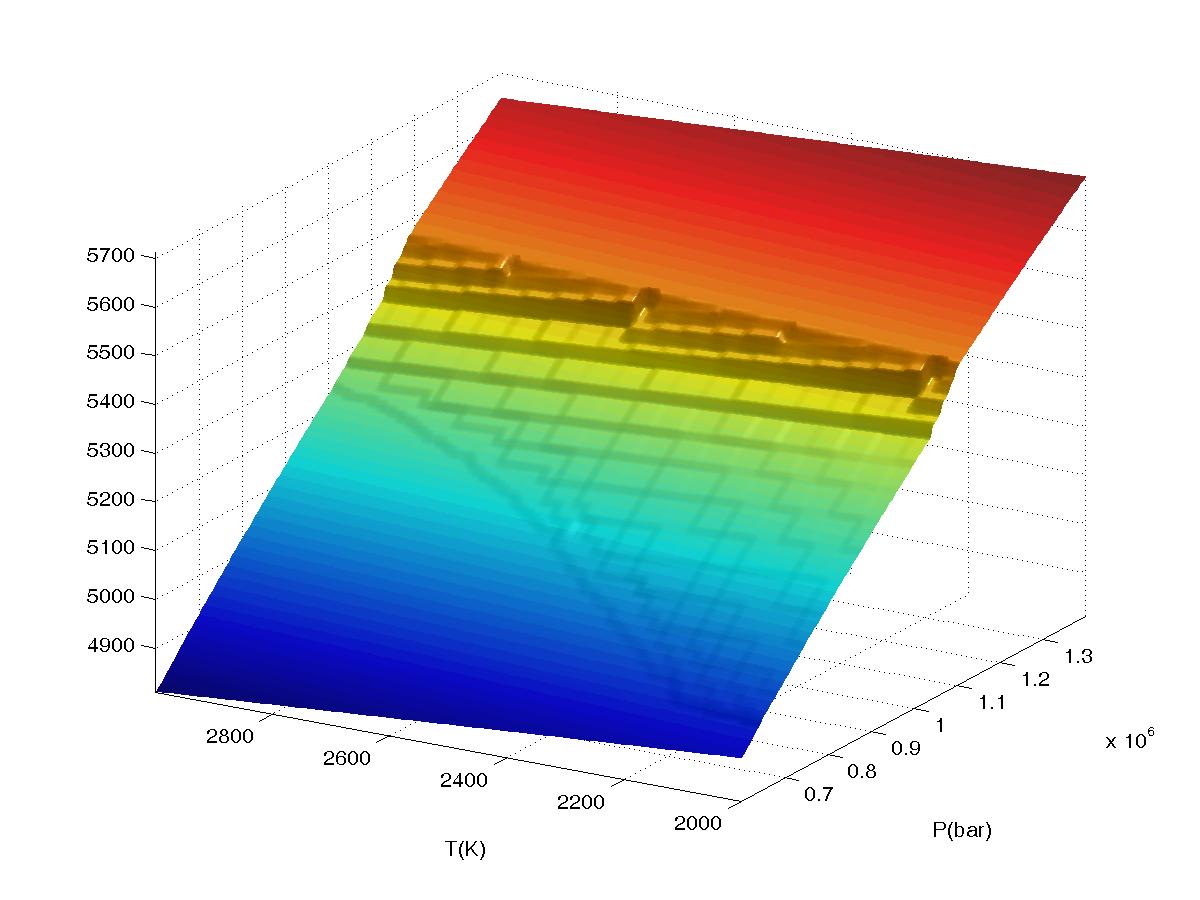
Figure 2. Plots of bulk density for a high pressure phase transformation as a function of interpolation range (value2), the calculation was done in VERTEX on a 4 level grid (JLEV=4) with 20x20 nodes at the lowest level of resolution and refinement of only true phase boundaries (the default grid refinement mode). The data was sampled on a 150x150 grid in WERAMI to create the plots. All plots were made with both interpolation and extrapolation on. The first plot shows results obtained for value2=0 (equivalent to "interpolation off") in which the underlying structure of the multilevel grid is clearly visible. Continued...

The second plot shows results obtained for value2=1, for JLEV=4 a unit increment in value2 corresponds to 8 grid nodes at the highest level of the computational grid. Continued...

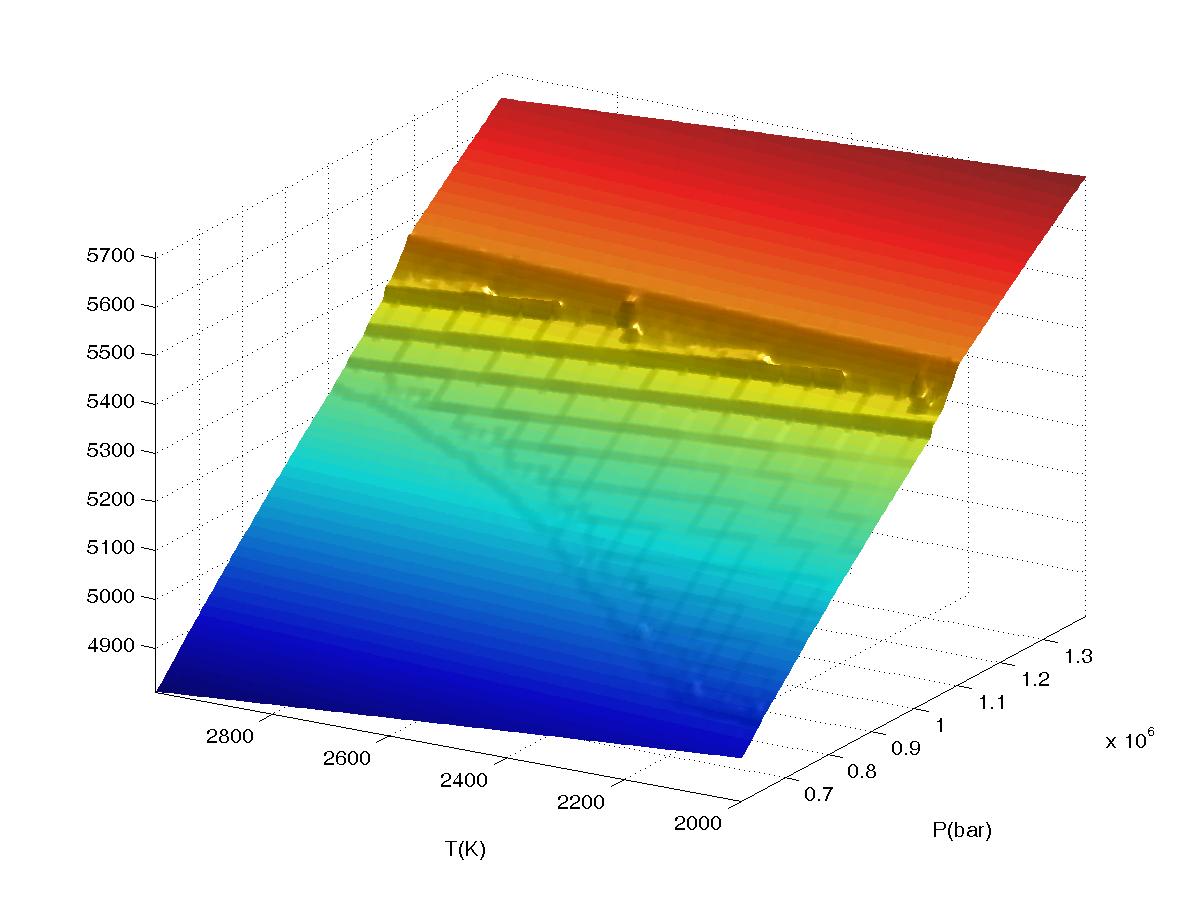
The third plot shows results obtained for value2=2 (the default value), with this choice the continuous variation in density is reasonably well represented. Although the surface appears eroded in places, probably a result of extrapolation. Continued...

 

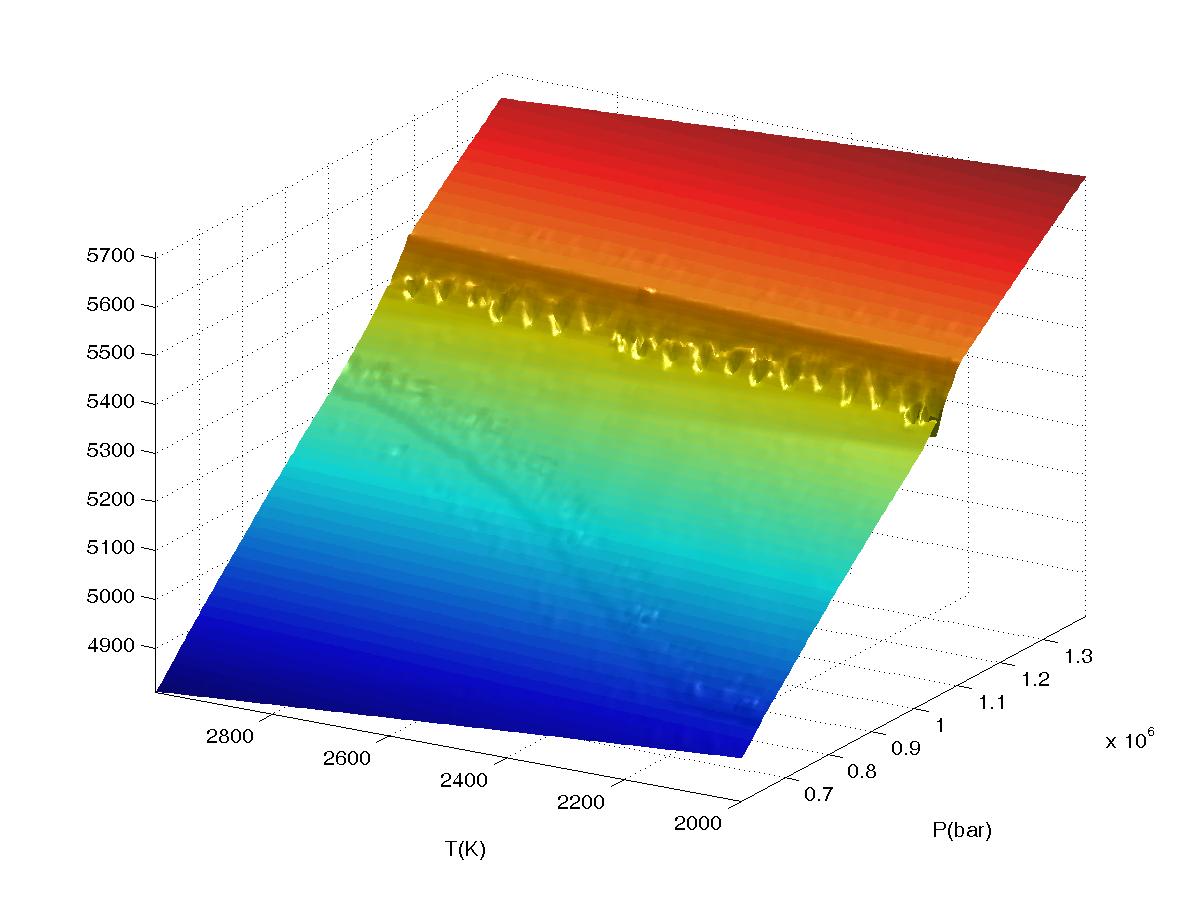
The fourth plot shows results obtained for value2=3, here the relatively long interpolation/extrapolation distances cause undesirable artifacts.

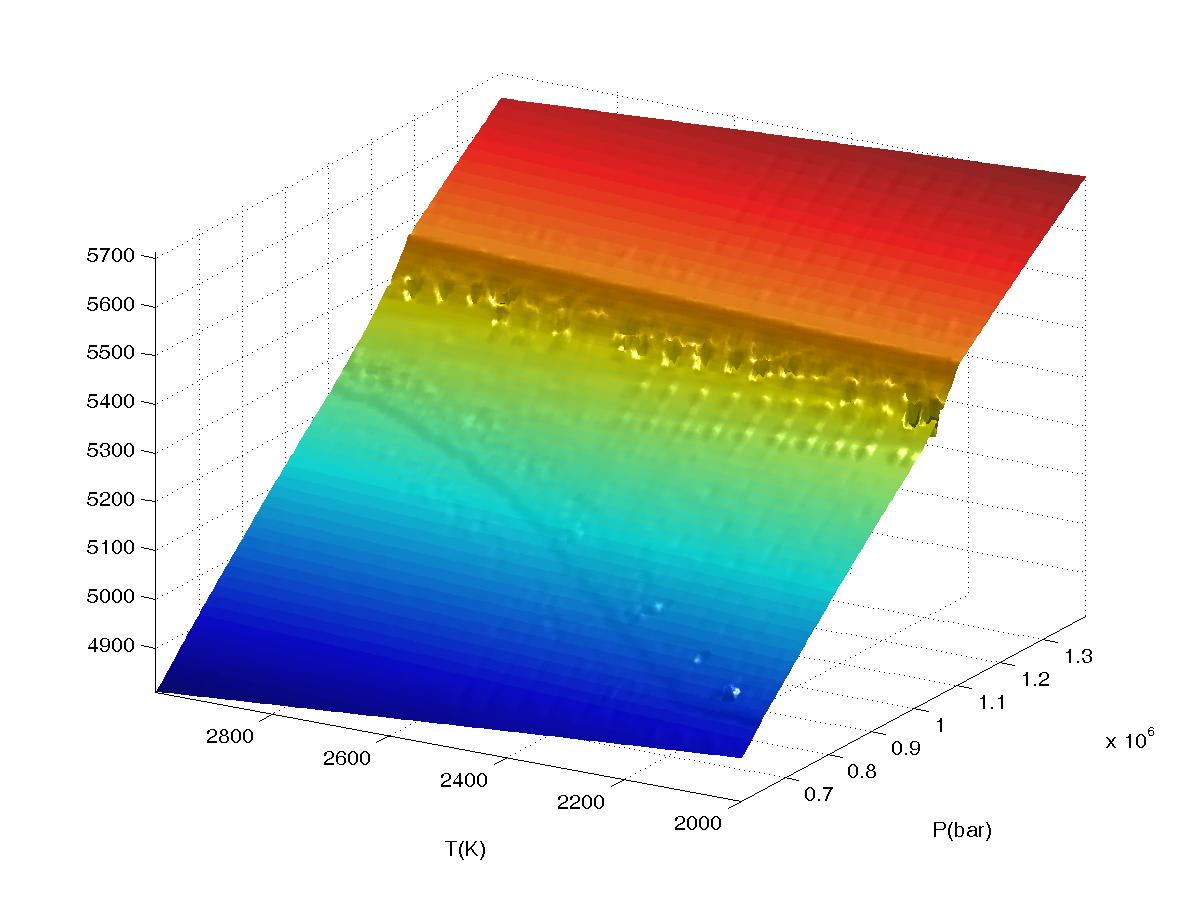
This keyword affects WERAMI.

keep_auto (obsolete 6.9.1+)

The keep_auto keyword controls whether the number of dynamically-generated compositions retained for each refinement point during adaptive optimization is automatically reduced if retaining the number of compositions specified by the keep_max option would exhaust allocated memory (error ver058). Once the threshold specified by keep_max has been reduced its original value is not restored during the remainder of a calculation. 

If keep_auto is F and VERTEX or MEEMUM exhausts the memory allocated for dynamically-generated compositions during an optimization, then the optimization is reported as failed (warning ver105) and, in the case of VERTEX, calculations continue.

NOTE: There is no benefit in setting keep_auto to F unless Perple_X is recompiled to increase the memory allocated for dynamically generated phase compositions (parameter k21 in perplex_parameters.h).

This keyword may take values: T (true) or F (false). The default is T.

This keyword affects VERTEX and MEEMUM.

keep_max (obsolete 6.9.1+)

The keep_max keyword specifies the maximum number of dynamically-generated compositions retained for each refinement point during adaptive optimization, keep_max is relevant only if keep_auto is T.

Although the intent of the keep_max/keep_auto options is primarily to prevent failed optimizations due to limited memory, in calculations with complex solutions, reducing keep_max may result in significantly faster calculations with little reduction in quality. Such effects are problem specific, but in general a value of 1'000 is adequate, values below 100 may lead to a notable deterioration in quality and numerical instability.

keep_max takes integer values > 0, its default is 25000, recommended values are > 100, < k21/10, the value of k21 is specified in perplex_parameters.h and is generally > 500000.

NOTE: to maximize computational quality set keep_max to a large_number (e.g., 5000000). Perple_X will then reduce keep_max (warning ver058) as necessary. If keep_max is automatically reduced to a low value (<~20000) it is likely that the problem is poorly configured or that Perple_X has been compiled with inappropriate paramters (perplex_parameters.h).

This keyword affects VERTEX and MEEMUM.

linear_model

If the linear_model keyword is on phase boundaries are assumed to be linear between grid nodes at the active level and next sublevel of a multilevel grid during gridded minimization calculations. This assumption, which was used in the original gridded minimization strategy (Connolly 2005), results in a reduction in the number of calculations because it implies that if the same assemblage is present at two adjacent nodes at the current level of resolution, then the assemblage must also be present at the intervening node at the next sublevel. The assumption is not rigorous and may result in step-like boundaries, a problem that can be avoided by setting the keyword value to off. When linear_model is off, the multilevel gridding strategy is identical to the wavelet strategy described by Gerya et al. (EPSL, 2004). For 2-dimensional grids, setting linear_model to off increases computation time and output file size roughly twofold.

This keyword affects VERTEX.

logarithmic_p

The logarithmic_p keyword controls whether the nominal value of the pressure variable is interpreted as pressure or its base 10 log. If logarithmic_p is T, the thermodynamic pressure for calculations is computed as log₁₀P; thus for a calculation with pressures ranging from 10^-5 to 10² bar, the user enters values of -5 and 2 for the minimum and maximum pressure.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects WERAMI, MEEMUM, and VERTEX.

logarithmic_X

The logarithmic_X keyword controls whether the nominal value of the saturated phase compositional variable X (usually Y_CO2, the composition of a binary H2O-CO2 fluid) is interpreted as a composition or its base 10 log. If logarithmic_X is T, the compositional variable for calculations is computed as log₁₀X; thus for a calculation with X ranging from 10^-5 to 10⁰ mole, the user enters values of -5 and 0 for the minimum and maximum X. 

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects WERAMI, MEEMUM, and VERTEX.

LP_max_it

The LP_max_it keyword sets max number of iterations for a single LP optimization. 

This keyword may take positive integer values. The default is 500.

This keyword affects MEEMUM and VERTEX.

low_reach (obsolete 6.9.1+)

NOTE: low_reach is a not a perplex_option.dat keyword, the low_reach keyword is an option that applies to a specific solution model. To implement this keyword modify the solution model file by adding the keyword to the text of the relevant solution model prior to the end_of_model keyword.

Presence of the low_reach keyword signals that the composition of a solution is to be discretized by only two points about a refinement point during the iterative stage of an adaptive optimization. For a solution with an n-dimensional composition space this option reduces the usage of memory allocated for dynamic compositions by a factor of (2/3)^n compared to that required using the default value of the resolution_factor keyword. For a 10-dimensional solution, this effect reduces memory usage and computation time by nearly two orders of magnitude. Although these benefits are dramatic, they are offset by a notable reduction in quality; thus low_reach is an option of last resort.

low_reach conflicts with reach_increment, therefore both options should not be set in the same solution model. 

This keyword affects VERTEX and MEEMUM.

See also: final_resolution, resolution_factor, initial_resolution, solvus_tolerance, adaptive minimization keyword group discussion.

melt_is_fluid

The melt_is_fluid keyword controls whether WERAMI considers silicate melts to be fluids on output. If melt_is_fluid is F, then properties for the "solid" aggregate include melts.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects WERAMI and MEEMUM.

non_linear_switch (6.8.6+)

The non_linear_switch keyword toggles the default behavior of VERTEX, MEEMUM, and CONVEX with respect to the discretization parameter XINC used in non-linear subdivision schemes. See the commnentary in the header of the 6.8.6+ versions of solution_model.dat for explanation and discussion of this parameter. 

When non_linear_switch is F MEEMUM and VERTEX read XINC from the text of the individual solution models, otherwise XINC is equated to the appropriate value of the initial_resolution option. 

When non_linear_switch is F CONVEX equates XINC to the appropriate value of the initial_resolution option, otherwise XINC is read from the text of the individual solution models.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects VERTEX, MEEMUM, and CONVEX.

null_phases

The null_phases keyword controls whether CONVEX considers phases that consist entirely of mobile and/or saturated components (i.e., a null phase is a phase that contains no thermodynamic components). The keyword is relevant for calculations as a function of chemical potentials, activities, or fugacities. In such calculations phase relations are metastable with respect to null phases beyond the saturation surface. If null phases are considered, and a supersaturated initial condition is specified, then CONVEX will terminate with a message that there are no stable (pseudo-)univariant equilibria. To avoid this cryptic message it is best to first run such calculations without considering null phase stability. In chemical potential calculations the saturation surface can then be computed explicitly by considering null phase stability. In activity/fugacity calculations the saturation surface cannot be defined explicitly, but allowing null phases will eliminate metastable equilibria. For example, if a phase diagram is computed for the CaO-MgO-SiO₂ system as a function of activity of periclase and quartz, then at pressure-temperature conditions where forsterite is stable the condition a(per) = a(qtz) = 1 is supersaturated with respect to forsterite; if the same calculation is done as a function of μ(SiO₂) and μ(MgO), then the forsterite saturation surface will be computed if null phases are allowed.

Null phases are not permitted in calculations as a function of chemical potentials, activities, or fugacities with VERTEX. Therefore users should be aware that the phase equilibria resulting from such calculations may be metastable with respect to null phases.

This keyword may take values: T (true) or F (false). The default is F.

option_list_files

The option_list_files controls whether VERTEX, MEEMUM and WERAMI output a text file that summarizes the option settings relevant for a calculation. If option_list_files = T, then files are output and named my_project_PROGRAM_options.txt, where "my_project" is the project name and PROGRAM is the name of the relevant program.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects VERTEX, MEEMUM and WERAMI.

order_check (obsolete 6.9.1+)

The isobaric-isothermal Gibbs energy of a solution model with non-convergent ordering may have several minima as a function of the model order parameters. These minima correspond to different equilibrium ordering states, the stable state being that with the lowest Gibbs energy. For such models, Perple_X is programmed to seek the minima corresponding to the most ordered state. If order_check is on, the energy of this state is compared to the fully disordered state, and the lowest energy is used for calculations. Under most conditions, this strategy gives the stable state of ordering for all conditions with a single solution model, but it has the disadvantage that the discontinuous transition between partially ordered and completely disordered phases (e.g., the tri-critical curve) is not shown explicitly. If order_check is off, the phase is always assigned the energy of the maximum order state; therefore in calculations were an order-disorder model and its fully disordered equivalent are both present (e.g., omphacite and clinopyroxene), Perple_X will explicitly delineate discontinuous order-disorder transitions.

If you do not understand the foregoing paragraph, then use the following rules:

1) If order_check = on and the calculation includes an order-disorder model, then it should NOT include the fully disordered equivalent (i.e., a calculation including omphacite, should NOT include clinopyroxene).

2) If order_check is off and the calculation includes an order-disorder model, then it SHOULD include the fully disordered equivalent (i.e., a calculation including omphacite, should include clinopyroxene).

This keyword affects VERTEX, WERAMI, and MEEMUM.

output_iteration_details

If output_iteration_details is true (T), then MEEMUM and VERTEX write information on the amount, stability, and composition of refinement points during each iteration of adaptive minimization calculations. This output provides diagnostic information on the quality of minimization results and resolution precision.

The default value of output_iteration_details is F. This keyword is intended primarily for interactive analysis with MEEMUM, setting output_iteration_details to F will substantially slow calculations with VERTEX because of the volume of output written to the console. 

See also: output_iteration_G, iteration, initial_resolution, final_resolution, adaptive minimization keyword group discussion

output_iteration_G

If output_iteration_G is true (T), then MEEMUM and VERTEX write the free energy of the system (per mole of the systems components) and the chemical potentials of its components after each iteration of adaptive minimization calculations. This output provides diagnostic information on the quality of minimization results and resolution precision.

Specifically:

1) The total free energy should converge smoothly to a minimum, increasing the number of iterations (e.g., by decreasing final_resolution) beyond this minimum does not improve the quality of the minimization.

2) Oscillation or increasing total free energy during iteration is an indication of a poor choice of optimization parameters (e.g., over-refinement).

3) If the free energies of the possible phases of the system are taken to be perfectly known, then the magnitude of a significant change in the total free energy of the system is comparable to the round-off error on the reference state Gibbs energies. Typical round-off error is ~100 J/mol. In general, the true error on reference state Gibbs energies is ~1000-10000 J/mol.

4) The precision of minimization may improve significantly even if the improvement in the total free energy of the solution is insignificant. This precision can be judged by comparing the variation in the chemical potentials during iteration to the precision of the data. Chemical potential variations can also be used to identify well- or poorly-resolved components.

To illustrate by example, the following output was generated from the bl478_benchmark, at 1050.15 K and 4000 bar, by increasing final_resolution to 1e-8 mole:

Iteration    G(J/mol)           H2O      MgO      Al2O3    K2O      CaO      TiO2     FeO      O2       Na2O     SiO2
    0       -926202.1570       -390238  -688844 -1794082  -956488  -804320 -1030145  -369515  -512236  -872061  -977953
    1       -926270.5179       -391218  -689244 -1794209  -956888  -804224 -1030236  -369536  -511872  -871984  -977953
    2       -926284.1030       -390927  -689271 -1794410  -963451  -804091 -1029920  -369108  -525225  -871658  -977953
    3       -926288.8551       -391376  -689223 -1794364  -956204  -804244 -1030109  -369072  -522614  -871797  -977953
    4       -926289.1760       -391263  -689187 -1794402  -958435  -804194 -1030001  -369150  -522853  -871746  -977953
    5       -926289.2590       -391231  -689123 -1794436  -958964  -804152 -1029899  -369190  -523849  -871721  -977953
    6       -926289.2753       -391253  -689107 -1794437  -958629  -804150 -1029890  -369180  -524257  -871728  -977953
    7       -926289.2797       -391256  -689108 -1794437  -958608  -804151 -1029893  -369179  -524208  -871726  -977953
    8       -926289.2811       -391255  -689109 -1794437  -958620  -804152 -1029894  -369179  -524190  -871726  -977953
    9       -926289.2816       -391255  -689108 -1794437  -958620  -804151 -1029893  -369179  -524204  -871726  -977953
   10       -926289.2817       -391255  -689108 -1794437  -958620  -804152 -1029893  -369179  -524207  -871726  -977953
   11       -926289.2818       -391255  -689108 -1794437  -958620  -804152 -1029893  -369179  -524204  -871727  -977953
   12       -926289.2818       -391255  -689108 -1794437  -958619  -804152 -1029893  -369179  -524207  -871727  -977953
   13       -926289.2818       -391255  -689109 -1794437  -958620  -804152 -1029893  -369179  -524204  -871727  -977953
   14       -926289.2818       -391255  -689109 -1794437  -958621  -804152 -1029893  -369179  -524204  -871727  -977953
   15       -926289.2818       -391255  -689109 -1794437  -958621  -804152 -1029893  -369179  -524204  -871727  -977953
   16       -926289.2818       -391255  -689109 -1794437  -958621  -804152 -1029893  -369179  -524203  -871727  -977953

The variation in total free energy indicates that the accuracy of the thermodynamic data does not justify more than 2-3 iterations (as obtained with initial resolution = 0.1 and final_resolution = 1e-2 mole). The variations in the chemical potentials indicate that O2 is the most poorly resolved component. Its variation becomes comparable to its precision after 6 iterations (as obtained with initial resolution = 0.1 and final_resolution = 1e-3 mole). To put these variations in perspective, a variation of 50 J/mol in the chemical potential of O₂ corresponds to a variation in oxygen fugacity of 2e-3 log10 units (50 J/mol /(2.303*R*T)).

The default value of output_iteration_G is F. This keyword is intended primarily for interactive analysis with MEEMUM, setting output_iteration_G to F will substantially slow calculations with VERTEX because of the volume of output written to the user console. 

See also: output_iteration_details, iteration, initial_resolution, final_resolution, adaptive minimization keyword group discussion.

pause_on_error

The pause_on_error (T or F) keyword determines whether Perple_X programs terminate upon encountering an anticipated error (F) or pause and wait for user interaction (T).

The default value of pause_on_error is T.

If a Perple_X program is being run via a script, or as a subroutine of another program, then pause_on_error should be set to ensure that in the event of an error Perple_X returns control to the calling script/program.

pc_perturbation

In Schreinemakers and mixed-variable diagram calculations (i.e., unconstrained optimization) compositional degeneracies among the pseudocompounds of different solutions (e.g., that pseudocompounds of different solutions may have exactly the same Fe/Mg ratio) may make it impossible for Perple_X to determine the true variance of pseudo-univariant and -invariant equilibria. To avoid this problem a small perturbation to the compositions of the pseudocompounds generated for each solution is introduced. The magnitude of the perturbation is proportional to the value assigned to the pc_perturbation keyword.

The default value of pc_perturbation is 5d-3. The sensitivity of Perple_X to this parameter has not been tested. The perturbation for each solution is calculated as delta = pc_perturbation * cst * initial_resolution, where cst is a random number between 1 and 10. It is expected that this method of eliminating degeneracies will be effective if delta is greater than the numerical resolution for compositions (~1d-5).

This keyword affects VERTEX.

poisson_ratio

The poisson_ratio keyword controls whether, and under what circumstances, a default value for the Poisson ratio is used to calculate shear moduli and seismic wave velocities.

The poisson_ratio keyword takes 2 values, value1 and value2

value1 may be on, off or all. The default is on

value2 is the value for the Poisson ratio, the default is 0.35

If value1 = off and no shear modulus is available for a phase, then the shear modulus and seismic velocities of the phase are assigned the bad_number value.

If value1 = on and no shear modulus is available for a phase, the shear modulus is computed as 3K(1-2ν)/(ν+1)/2, where the Poisson ratio ν = value2 and K is the bulk modulus. If no bulk modulus is available, then the shear modulus and seismic velocities of the phase are assigned the bad_number value.

If value1 = all, then the shear modulus of any phase is computed as 3K(1-2ν)/(ν+1)/2 regardless of whether other data are available for the shear modulus. If no bulk modulus is available, then the shear modulus and seismic velocities of the phase are assigned the bad_number value.

This option affects WERAMI, MEEMUM and FRENDLY. For calculations analyzed with WERAMI, changing this keyword does not necessitate repeating the primary calculation with VERTEX.

Other keywords relevant to seismic velocity calculations: vrh/hs_weighting, bounds, explicit_bulk_modulus, Anderson-Gruneisen, melt_is_fluid, interpolation, seimsic_data_file.

poisson_test

The poisson_test (T or F, default F) keyword activates an error trap that checks whether the poisson_ratio of a phase is negative. The most common cause of negative Poisson ratios in Perple_X is a data base configuration in which bulk moduli are computed from an isostatic EoS while shear moduli are computed from empirical functions. 

In general it is expected that the error trap will only be useful for applications where seismic wavespeeds are of primary concern. For such applications, running WERAMI with the error trap activated will identify conditions where the computed seismic wavespeeds are dubious.

This option affects WERAMI, MEEMUM and FRENDLY. For calculations analyzed with WERAMI, changing this keyword does not necessitate repeating the primary calculation with VERTEX.

proportions

The proportions keyword controls whether the relative proportions of phases (i.e., modes) are determined on the basis of weight or volume.

This keyword may take values: vol, wt. The default is vol.

This option affects WERAMI.

See also: composition_constant, composition_phase, composition_system

pseudocompound_file

The pseudocompound_file controls whether VERTEX outputs a text file that summarizes the static pseudocompound compositions used for a calculation. If pseudocompound_file = T, then the file is output and named my_project_pseudocompound_list.txt, where my_project is the project name and PROGRAM is the name of the relevant program.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects VERTEX and MEEMUM.

reach_increment (obsolete 6.9.1+)

NOTE: reach_increment is a not a perplex_option.dat keyword, the reach_increment keyword is an option that applies to a specific solution model. To implement this keyword modify the solution model file by adding the keyword and its value on the line prior to the end_of_model keyword (e.g., see Figure 4 in the adaptive minimization keyword group discussion).

The reach_increment keyword value specifies an incremental increase in the range over which the compositional variables of a specific solution phase are allowed to vary between successive iterations during adaptive minimization. The increase may improve the resolution of phase relations involving two or more solutions with extraordinarily flat free-energy composition surfaces. This circumstance is problematic, because a small error in the composition of one phase may cause a large error in the other phase. Most commonly this occurs when two or more coexisting phases are related by a solvus. This kind of error is manifest by spurious solvi, which typically have irregular or patchy boundaries. This issue is addressed in the adaptive minimization keyword group discussion.

To a good approximation, if at iteration n-1 the estimated composition of a phase is x_n-1±d_n-1, then in the subsequent iteration the composition will be allowed to vary approximately over the interval x_n-1±reach_increment*d_n-1. (see resolution_factor, eq [3]). The number of compositions considered during the iterative refinement of the composition of a solution with c compositional variables is proportional to

            [1+ resolution_factor + 2*reach_increment]^c-1

Thus, large reach_increment values are particularly expensive in terms of both memory usage and time for complex solutions (e.g., silicate melts).

The default value for reach_increment is 0. If reach_increment for a specific solution model is > global_reach_increment, then the local value overrides the global value. Experience suggests that a value of 6 is adequate to resolve phase relations involving silicate solvi if the initial resolution value for adaptive minimization is in the range 1/10 - 1/50. 

This keyword affects VERTEX and MEEMUM.

See also: low_reach, final_resolution, resolution_factor, initial_resolution, solvus_tolerance, adaptive minimization keyword group discussion.

reach_increment_switch (obsolete 6.9.1+)

The reach_increment_switch keyword controls how reach increments specified by the reach_increment and/or global_reach_increment keywords are implemented.

The reach_increment_switch keyword may take the following values:

off  - all reach increments are set to zero

on   - reach increments are applied only during the auto-refine stage of calculations with VERTEX

all  - reach increments are applied during both the exploratory and auto-refine stage of calculations with VERTEX

The default is on. 

Setting reach_increment_switch to all improves the compositional resolution obtained during the exploratory stage, in general this improvement is expected to be insignificant and increases both the time and memory required for the exploratory stage. 

For calculations with MEEMUM reach increments are used regardless of whether auto-refine data is being used unless reach_increment_switch is set to off.

This keyword affects VERTEX and MEEMUM.

reaction_format

The reaction_format keyword controls the output format for reactions identified in Schreinemakers and mixed variable diagram calculations.

This keyword may take the following values:

minimum    - only phases in the thermodynamic composition space are output

full       - phases in the saturated component composition space are also output

stoich     - stoichiometric coefficients are also output

S+V        - entropy and volume are also output

everything - everything is output

The default is minimum.

WARNING: full reaction equations vary as a function of the independent variables as these variables may cause the entropy and volume of a reaction and the identity of stable saturated phases to change. The equations output are those at the first equilibrium condition found.

This keyword affects CONVEX.

reaction_list

The reaction_list keyword controls whether a spreadsheet formatted list of reactions found during Schreinemakers and mixed variable diagram calculations.

This keyword may take values: on, off. The default is off.

This keyword affects CONVEX.

refine_endmembers (option file)

The refine_endmembers keyword controls whether the endmember compositions of a solution are accepted as refinement points during optimization. 

This keyword may take the value T or F.

This keyword affects VERTEX and MEEMUM.

refine_endmembers (solution model file keyword)

NOTE: refine_endmembers is not a perplex_option file keyword, rather it is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the keyword before the end_of_model keyword.

If the refine_endmembers keyword is present in a solution model, then the solution model is evaluated to compute the properties of the solution at its endmember bulk compositions.

Prior to version 6.7.8, Perple_X did not evaluate solution models for the composition of a pure endmember, the assumption being that the properties predicted by the solution model at the endmember bulk composition would be identical to the those of the pure endmember. This assumption is not valid for order-disorder models in which order-disorder is possible at an endmember bulk composition. In such cases, if refine_endmembers is not specified Perple_X will return the property of the fully ordered endmember at the endmember composition, rather than the property of the endmember with the stable state of order. For example, the Ilm(WPH) model represents order-disorder in terms of an ordered endmember (oilm) and a disordered endmember (dilm). If no refine_endmembers keyword is present in the model, Perple_X returns the properties of oilm for the pure ilmenite bulk composition, but if the refine_endmembers keyword is added to the model, then the properties obtained for the pure ilmenite bulk composition correspond to an equilibrium mixture of ordered (oilm) and disordered ilmenite (dilm) species. 

Currently (6.7.8) there are only two solution models [Ilm(WPH) and Cpx(G)] in the standard solution model file (solution_model.dat) where order-disorder occurs in the limit of an endmember bulk composition. The refine_endmembers keyword has been added to the Ilm(WPH) model and it must be added to the Cpx(G) model if Cpx(G) is to be used to compute properties at the bulk Ca-Tschermaks endmember composition.

refinement_points

The refinement_points keyword specifies the number of metastable, i₂, compositions that are to be refined during adaptive optimization. Reducing the value of this keyword substantially reduces the cost (in both memory and time) of calculations, but ultimately may lead to poorly resolved phase boundaries. Prior to Perple_X 6.7.6, the number of metastable refinement points was equal to the number of thermodynamic components. From 6.7.6 through 6.8.0 refinement_points defaulted to 5. As of 6.8.1, the default behavior is equivalent to assigning the aut (automatic) value. 

Unnecessarily large values of this keyword may substantially increase the cost of calculations in both time and memory, while small values may lead to poorly resolved phase boundaries and/or numerical instability.

In the initial optimization (iteration 0) of an adaptive optimization metastable phase compositions are chosen by selecting the least metastable composition of each solution, subject to the caveat that if a composition of the solution is stable, the metastable composition must be separated from the stable composition by a distance > solvus_tolerance_II. The resulting list of metastable phase compositions is then sorted in order of increasing metastability and the first i₂ compositions of this list are taken for subsequent refinement. In subsequent iterations, the metastable refinement points are selected from the compositions associated with the metastable refinement points of the previous iteration and ranked by stability.

If this keyword is assigned the aut (automatic) or default value refinement_points is set to a minimum value of 5. If c + 2 (c is the number of thermodynamic components specified for a calculation) > 5, then refinement_points_II is set to c + 2. If refinement_points is assigned an integer value in the option file, the specified value is not modified regardless of the number of thermodynamic components.

This keyword affects VERTEX and MEEMUM.

See also: low_reach, final_resolution, reach_increment, initial_resolution, iteration, solvus_tolerance, adaptive minimization keyword group discussion, refine_switch.

refine_switch

The refine_switch keyword controls whether metastable refinement points corresponding to a stable phase are retained during the iterative stages of an adaptive optimization. For problems involving complex solutions, setting this switch to F may substantially reduce the usage of memory allocated for dynamic compositions, accelerate calculations, and, counter-intuitively, improve the resolution of phase boundaries. In simpler problems, setting this switch to T marginally improves the resolution of phase boundaries. 

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects VERTEX and MEEMUM.

See also: low_reach, final_resolution, reach_increment, initial_resolution, iteration, solvus_tolerance, adaptive minimization keyword group discussion, refinement points.

refinement_threshold (obsolete 6.7.8+)

The refinement_threshold keyword can be used to specify a threshold in Gibbs energy beyond which metastable phase compositions will be eliminated during adaptive optimization. Specifically, if g_i - sum(x_ijm_j) > refinement_threshold, then the composition is eliminated, where m_j are the chemical potentials of the current solution. This may seem like a good idea. It is not. In systems with a large number of thermodynamic components, a highly metastable composition may become stable in successive iterations. 

Setting the refinement threshold to near zero (e.g., 1e-4 J) may result in a several orders of magnitude reduction in the amount of memory required during adaptive optimization, but causes only minor reduction in computation time. The fraction of the total number of compositions eliminated by application of the threshold is indicated by the console message:

   Metastability filtering eliminated XX.XXX% of the trial compositions prior to optimization.

written when VERTEX finishes a calculation. Small values may lead to numeric instability that is manifest by splotchy phase diagram sections and failed optimizations. The value that qualifies as "small" is problem specific and for that reason it is not recommended for inexperienced users.

This keyword takes a numeric value (< 12 characters): >0, and defaults to 1d4. If refinement_threshold > 1d4, then the threshold is deactivated. 

This keyword affects VERTEX and MEEMUM.

See also: final_resolution, reach_increment, initial_resolution, iteration, solvus_tolerance, adaptive minimization keyword group discussion.

resolution_factor (aka, iteration) (obsolete 6.9.1+)

Prior to version 6.8.4 the iteration keyword took two values, in 6.8.4+ the second value is specified by refinement_points and the first value identified as resolution_factor. Eqs [3,4] have been modified for 6.8.4+ to account for the change in the way reach_increment is implemented.

In versions after 6.8.3, but with a time stamp earlier than October 3, 2019, the range parameter was half the value indicated by Eq [1] below, to obtain comparable quality to calculations made with those versions with current versions the refine_factor keyword should be increased to 3.

resolution_factor influences the accuracy with which the compositions of coexisting phases are determined during adaptive minimization (MEEMUM and VERTEX, Connolly 2009). In adaptive minimization, the composition of any solution phase is initially discretized with compositional resolution d₀. and stable compositions are iteratively refined until the precision is better than the value of the final_resolution keyword. The initial resolution is not necessarily constant, even for a given compositional variable in a particular phase (see subdivision_schemes). However, most commonly, the resolution for all solution models is constant and determined by initial resolution keyword (i.e., for Cartesian subdivision). For Cartesian subdivision

            d₀ = initial resolution. 

The specific resolution formulae given below assume Cartesian subdivision.

In iteration n of an adaptive minimization, the compositional variable of a phase is allowed to vary discretely over the range ±r around the estimated composition x_n-1. The value of the resolution_factor keyword, in combination with d₀, determines both the minimum value of r

and the actual resolution of the discretization

            d_n = 2r_min/resolution_factor.                            [2]

For a calculation with a single, miscible, solution phase, at iteration n-1, a composition of the solution phase x_n-1 is determined with precision ±d_n-1. Thus at iteration n, the refined composition x_n will lie within the interval x_n-1±d_n-1. This simple model is usually reasonable when multiple solution phases coexist. The exception being in the case that the free-energy composition surfaces of the phases are extraordinarily flat, as when two or more coexisting phases are related by a solvus. Solvi are problematic because a small error in the composition of one phase may cause a large error in the other immiscible phases. In such circumstances it is helpful to widen the interval over which a solution may change its composition between iterations. To permit this, the interval half-width is computed as

            r_n = r_min + reach_increment.           [3]

The number of discretization points for the compositional variable is then

            p = 1 + resolution_factor + 2 * reach_increment             [4]

Large values of resolution_factor increase the time and memory required for each iteration, but because the rate at which resolution increases with each iteration also improves with resolution_factor, fewer iterations are required to achieve the target precision (final_resolution). Calculations done with larger values of resolution_factor are slightly more precise. resolution_factor must be an integer > 1, its default value is 3, experience suggests that this value is usually optimal. Changing the value of resolution_factor to resolution_factor' changes the total number of compositions evaluated by a factor of roughly as (resolution_factor/resolution_factor')^c;  for a nine component solution this implies reducing resolution_factor from 3 to 2 will result in a ~38-fold reduction in the total number of compositions evaluated during an optimization and a comparable reduction in the amount of memory required for optimizations. If the evaluation of the EoS of the solution is costly (e.g., in the case of order/disorder models), this reduction translates directly as a translation in computational time with a relatively minor reduction in the quality of the resulting calculation. The related reduction in memory is one way of solving the problem indicated by the VERTEX error message **error ver058**.

The resolution_factor keyword takes a real value. It currently defaults to the minimum permitted value (2), prior to version 6.8.4 the default value of resolution_factor was 3.

During adaptive optimization, subdivision using even values of resolution_factor reproduce the refinement point composition exactly, whereas odd values cause new compositions to be displaced slightly from the refinement point composition. I have not tested the consequence of this difference, but my intuition is that even values should give better results. The factor 2 on reach_increment in [4] assures reach_increment does not break the even/odd symmetry. 

This keyword affects VERTEX and MEEMUM.

See also: low_reach, final_resolution, reach_increment, initial_resolution, refinement_points, output_iteration_G, solvus_tolerance, adaptive minimization keyword group discussion.

sample_on_grid

VERTEX computes phase equilibria and physical properties on multi-level computational grid. If sample_on_grid is set to T, then WERAMI (in computational mode 2) samples results on the nodes of the computational grid used by VERTEX. The advantage of using this option is that it minimizes interpolation error. Set sample_on_grid to F to sample data on an arbitrary grid (e.g., to restrict the range of sampling). sample_on_grid has no effect on the sampling of 1-dimensional grids (WERAMI computational mode 3); in Perple_X 6.8.5+, 1-dimensional grids are always sampled on the maximum resolution computational grid used by VERTEX. Note that only the lowest computational grid used by VERTEX is fully populated by data; sampling at higher levels normally involves interpolation.

This keyword may take values: T (true) or F (false). The default is T.

This keyword affects WERAMI.

seismic_data_file

The seismic_data_file keyword controls whether a file summarizing the options relevant to seismic wave-speed calculations is output. If requested the file is written to my_project_seismic_data.txt, where my_project is a place holder for the project name. The file indicates options specified in perplex_option.dat and provides lists that indicate how these options are applied to the individual endmembers and solution models included in a calculation. The file is written whenever WERAMI, MEEMUM, or VERTEX is executed, therefore caution should be exercised to ensure that the file is not locked by an editor when these programs are run.

This keyword may take values: T (true) or F (false). The default is T.

This keyword affects VERTEX, MEEMUM, and WERAMI.

seismic_output

The seismic_output keyword controls the amount of information relevant to seismic wave propagation that is output by the programs WERAMI (in computational mode 1), MEEMUM and FRENDLY. 

This keyword may take values: all, some, none. The default is some, in which case the aforementioned programs output wave speeds and adiabatic shear and bulk moduli. If seismic_output = all, then the partial derivatives of wave speed and elastic moduli with respect to temperature and pressure are also output. These derivatives do not account for variations in the equilibrium mineralogy as a function of temperature or pressure. 

short_print

The short_print keyword controls whether equilibrium conditions of reactions found during Schreinemakers and mixed variable diagram calculations are output (provided a print file is requested).

This keyword may take values: on, off. The default is on.

This keyword affects CONVEX.

reject_bad_composition (solution model file)

NOTE: reject_bad_composition is not a perplex_option file keyword, rather it is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the keyword before the end_of_model keyword.

...

site_check obsolete 6.7.7+

The site_check keyword controls whether Perple_X rejects solution model compositions that yield negative site fractions.

This keyword may take values: T (true) or F (false). The default is T, i.e., negative site fractions are rejected.

The site populations of a valid solution model must be both positive and a linear combination of the site populations of its independent endmembers. A number of solution models implemented by Holland & Powell (JMG 1998, and various coworkers) in THERMOCALC, most commonly models involving Tschermaks substitutions, assume endmembers that are inconsistent with these requirements. To remedy this inconsistency Holland & Powell impose an ad-hoc correction, referred to as "equipartition", to the site fractions used to compute configurational entropy. Such ad-hoc corrections are not possible in Perple_X, therefore Perple_X and THERMOCALC may give different results. These differences can be reduced by setting site_check = F (false).

If site_check = F ,then Perple_X allows solution compositions that imply negative site fractions. For such compositions the configurational entropy is computed using only the positive site fractions generated by the invalid model. Thus in this case, Perple_X allows the same range of solution compositions as THERMOCALC, but does not necessarily compute the same configurational entropy. If site_check = T, the compositional range of the solution in Perple_X is restricted compared to the range allowed in THERMOCALC. With site_check = F results obtained using Perple_X tend to be more similar to those obtained with THERMOCALC than they are when site_check = T. Before April 2009, Perple_X operated as though site_check = F. Therefore Perple_X results obtained before that date can only be reduced with the current version if site_check is set explicitly to F.

WARNING: Setting site_check = F prevents Perple_X from testing for invalid site fractions that arise for reasons unrelated to the equipartition assumption.

site_check_override (solution model file)

NOTE: site_check_override is not a perplex_option file keyword, rather it is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the keyword before the end_of_model keyword.

If the site_check_override keyword is present in a solution model, then the tests for invalid dependent endmember site populations introduced in Perple_X 6.7.7 (see Perple_X 6.7.7 for explanation) are overridden and the solution model is treated in earlier versions of Perple_X. Specifically, if site_check_override is present in a model, then dependent endmember properties are computed according to their stoichiometric definitions in the solution model file and the only constraint on their concentration in the solution is that no atomic site fraction can be less than zero.

The site_check_override is useful for solution models in which order-disorder effects are partially or entirely accounted for by ad-hoc assumptions (e.g., Holland & Powell's, 2007, equipartition assumption). 

Currently (6.7.8) site_check_override has been added to the following solution models in the standard solution model file (solution_model.dat): Atg(PN), Amph(DHP), Amph(DPW), Bio(TCC), Chl(HP), GlTrTsPg, GlTrTsMr, Na-Amph. 

solution_names

The solution_names keyword determines whether Perple_X uses solution model names, abbreviations, or full_names on output.

This keyword may take the value mod[el], abb[reviation], or ful[l], the default is mod. The keyword has no effect for solution models that do not include the optional abbreviation and full_name keywords.

This keyword affects WERAMI, PSSECT, and MEEMUM.

solvus_tolerance

The solvus_tolerance keyword specifies the minimum distance (in normalized composition space) between two compositions of a solution phase at which the compositions are considered to represent distinct (immiscible) phases of the solution. Compositions that are separated by a distance less than solvus_tolerance are considered to represent a single phase whose composition is computed as the weighted average of the different compositions of the solution. 

This keyword takes the character value aut (automatic) or numeric values between 0 and 1, it defaults to aut.

solvus_tolerance = aut is almost always optimal. 

Set solvus_tolerance = 0 to prevent VERTEX from homogenizing stable pseudocompounds that represent a miscible phase (all phase assemblages will consist of p=c pseudocompounds). Set solvus_tolerance = 1 to make VERTEX homogenize all stable pseudocompounds of a given solution into a single phase regardless of whether or not the pseudocompounds represent distinct immiscible compositions.

MEEMUM/VERTEX 6.9.1+: If solvus_tolerance = aut, then the solvus tolerance is set to 10^-2 mol.

CONVEX: If solvus_tolerance = aut, then the solvus tolerance is to 3/2 * initial_resolution.

MEEMUM/VERTEX 6.9.0-: For adaptive minimization calculations the most common problems, i.e., spurious and stepped solvi, that occur during the calculation of solvus phase relations can resolved, respectively, via the reach_increment and solvus_tolerance_II keywords. The default value for solvus_tolerance (auto), results in a much coarser resolution for adaptive minimization than specified by final_resolution. The reason this coarse resolution is used as the default is that Perple_X may have difficulty converging to the correct compositions of coexisting immicible phases. These difficulties (see Figure 2b of the adaptive minimization keyword group discussion) arise because the algorithm assumes that if phase compositions have been discretized with resolution d_n, then the accuracy for any compositional variable x_n is ±d_n. Therefore during iterative refinement the compositional estimate is not allowed to move outside the interval x_n±d_n, this has the consequence that if two compositions are, in reality, miscible, but separated by a distance > d_n, the compositional estimates cannot converge during iteration. By improving the effective initial resolution and/or implementing the reach_increment option as described in the adaptive minimization keyword group discussion solvus_tolerance can be reduced to 3/2 * resolution_factor * final_resolution.

This keyword affects CONVEX, VERTEX, and MEEMUM.

solvus_tolerance_II

If you do not understand what this keyword does, then do not change it. 

This parameter can be adjusted to eliminate "stepped" solvus boundaries along which the compositions of the coexisting phases change by increments more closely related to the initial_resolution than to the final_resolution keyword values. 

The solvus_tolerance_II keyword sets an internal parameter that is used to select metastable phase compositions for subsequent refinement during adaptive minimization. If in an iteration of an adaptive minimization calculation, a composition of a solution phase is found to be stable, then metastable compositions of the solution will only be considered in the subsequent iteration if the metastable composition is separated from the stable composition by a distance greater than the value of solvus_tolerance_II.  The idea behind this keyword is that if a solution is immiscible, forcing Perple_X to consider phases far from a composition of perceived stability increases the likelihood that the algorithm will identify the multiple stable phases of a solution. This strategy does seem to improve the resolution of phase boundaries involving solvi, but for reasons that are unclear to me it also seems to improve the resolution of phase boundaries in general. The optimal value for this keyword should be problem specific, but experience with silicate solutions seems to suggest that the optimal value for this parameter is 0.25+/-0.05 regardless of the phases under consideration.

A disadvantage of using the relatively large default value for solvus_tolerance_II is that it may give rise to a numerical artifact in Perple_X referred to here as stepped solvi (See Figure 7 of the adaptive minimization keyword group discussion for an illustration of a stepped solvus). This problem occurs when the distance between the limbs of a solvus are less than the value of  solvus_tolerance_II, in this limit the tolerance prevents the adaptive minimization algorithm from refining compositions of immiscible phases that are perceived to be metastable. As a consequence the limbs of the solvus are only located accurately when the compositions generated at the lowest level of resolution (i.e., as determined by the effective initial resolution) are fortuitously close to stable compositions on the limbs of a solvus. The limbs of a solvus affected by this problem typically change in abrupt steps that correspond to steps in the compositions of the immiscible phases that are comparable to the initial_resolution. An additional disadvantage of setting solvus_tolerance_II to values greater than the effective initial resolution is that it limits the range over which a stable phase composition may change during adaptive refinement (this limitation can be overcome by using reach_increment). 

Perple_X's adaptive minimization algorithm is such that it is expected that non-zero values for this keyword improve the resolution of solvi, but degrade the resolution of normal phase boundaries by limiting the range over which phases may change their composition between iterations. 

This keyword affects VERTEX and MEEMUM.

See also: final_resolution, iteration, initial_resolution, reach_increment.

speciation_max_it

The speciation_max_it keyword specifies the maximum number of iterations permitted for solution of speciation (aka order-disorder) calculations, other iterative equations of state, and iterative solution of pseudo-univariant equilibrium conditions (CONVEX).

This keyword takes an integer value (>0) and defaults to 100.

This keyword affects VERTEX, CONVEX, FLUIDS, FRENDLY, WERAMI and MEEMUM.

speciation precision

The speciation_precision keyword specifies the precision of non-GFSM fluid speciation calculations.

This keyword takes a numeric value (< 12 characters): <1, and defaults to 1e-5 mol.

This keyword affects VERTEX, CONVEX, FLUIDS, FRENDLY, WERAMI and MEEMUM.

speciation_factor (obsolete 6.9.1+)

The speciation_factor keyword determines the precision of speciation calculations, this precision is computed as the effective final resolution divided by the speciation_factor. A value of 100 is usually adequate. The optimal value of this keyword can be determined by calculating the total Gibbs energy (with MEEMUM) of a system at a fixed pressure-temperature condition as a function of the speciation_factor. The smallest value of the speciation_factor at which no significant variation in the total Gibbs energy occurs is the optimal value.

Unnecessarily large values of this keyword may substantially slow calculations, while small values may lead to numerical instability. 

This keyword takes a numeric value (< 12 characters): >10, and defaults to 100.

This keyword affects VERTEX, CONVEX, FLUIDS, FRENDLY, WERAMI and MEEMUM.

speciation_tolerance (obsolete 6.7.6+)

This keyword is obsolete in post 6.7.5 versions of Perple_X, see speciation_factor.

The speciation_tolerance keyword specifies the precision of speciation calculations for order-disorder models, i.e., the permitted error in the molar fraction of an ordered species. Prior to Perple_X version 6.6, the value (10^-5) of this tolerance was specified internally. Typical enthalpies of ordering are in the range 10³-10⁴ J/mol; thus a tolerance 10^-5 of implies error of <10^-1 J/mol in the computed energy of phases described by order-disorder speciation models. Given that input energies are typically rounded to the nearest 10² J/mol, a speciation_tolerance of 10^-2 may be adequate for most purposes. The advantage of using a large tolerance is that it may accelerate calculations involving multiple order parameter solution models (e.g., Diener et al. 2007; Green et al., 2008), the disadvantage of specifying a large tolerance is that it may increase the roughness of computed properties.

This keyword takes numeric values (< 12 characters): >0, <1, and defaults to 10^-3.

This keyword affects VERTEX, CONVEX, FLUIDS, FRENDLY, WERAMI and MEEMUM.

species Gibbs energies

The species_Gibbs_energies keyword controls whether endmember Gibbs energies are output by MEEMUM and WERAMI.

This keyword may take values: T (true) or F (false). The default is F.

This keyword only affects WERAMI and MEEMUM.

species_output

The species_output keyword controls whether phase speciation is output by WERAMI (computational mode 1) and MEEMUM.

This keyword may take values: T (true) or F (false). The default is T.

This option only affects WERAMI and MEEMUM.

spreadsheet

The spreadsheet keyword controls whether WERAMI includes the independent variables of a calculation in tabulated output. Setting spreadsheet = T (true) results in larger output files, but is useful if the data is to be imported into a spreadsheet program (e.g., Excel).

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects mode 2 calculations in WERAMI.

stretch_factor and Non-Linear Subdivision 

The description of this option is out-of-date as of the 6.8.1 version of Perple_X, refer to the header commentary in a 6.8.7+ version of solution_model.dat for a discussion of the non-linear subdivision parameters. The mathematical form of the stretching transformation given below remains correct, however only IMOD = 1 is currently supported and the transformation is no longer mapped to [XMIN XMAX].

The post-3/21/07 version of Perple_X '07 allows four different models for discretizing the composition of a solution phase. These models, designated "subdivision schemes" are specified by a line in the solution model file for each independently variable endmember consisting of four numbers, XMIN, XMIN, XINC, and IMOD: XMIN and XMAX are the compositional limits of the solution; the (initial) number of discrete compositions (i.e., pseudocompounds) is calculated from XINC (if the initial_resolution keyword is specified, then the initial_resolution overrides the value of XINC specified locally in the solution model) as (XMAX-XMIN)/XINC + 1; and the spacing of these compositions is determined by IMOD as follows:

IMOD = 0 - Cartesian subdivision, XINC is the (initial) compositional spacing for the discretization.

IMOD = 1 - asymmetric transform subdivision, compositions are closely spaced towards XMIN.

IMOD = 2 - symmetric transform subdivision, compositions are closely spaced towards both XMIN and XMAX.

IMOD = 3 - double symmetric transform subdivision, compositions are closely spaced towards XMIN and XMAX and a third composition that is specified on the line following IMOD.

IMOD = 4 - asymmetric transform subdivision, compositions are closely spaced towards XMAX.

For IMOD=1-4, if the compositional domain is normalized so that W=0 and W=1 represent, respectively, the compositions at which compositions are closest and furthest apart, compositions are computed as W = ([1 - Z]*stretch_factor + 2)/(1 + Z) where Z = (stretch_factor + 2)**(1-Y) and Y = 0...1 at constant intervals of dY ~ XINC/(XMAX-XMIN). The exact relation between X and the composition generated depends on the way W is mapped to X, but to a first approximation, if the stretch_factor is 0.0164 the resolution of the solution will be improved by an order of magnitude where the spacing is smallest compared to Cartesian subdivision (IMOD=0). A consequence of this improvement, is that the resolution of the solution becomes worse (by more than a factor 2) where the spacing is largest. Increasing the stretch_factor to values > 1, results in a discretization scheme that is effectively Cartesian, whereas decreasing the stretch_factor by a factor of 2 increases the maximal compositional resolution by roughly an order of magnitude. Thus, values << 0.0164 may destabilize adaptive minimization, while values >> 0.0164 are unlikely to offer any advantage over the more straightforward Cartesian scheme (IMOD=0).

Pros and cons of non-linear subdivision (IMOD=1-3): The main advantage of using non-linear subdivision (in particular IMOD=1), is that it permits high resolution of minor elements (typically Mn, Cr, and Ti) that may strongly influence the location of phase boundaries. Calculations of solvi are often sensitive to extremal compositions of a solution, thus the accuracy of such calculations is improved by specifying IMOD=2 for the relevant solutions, the price paid for this choice is that the calculation has lower resolution far from the compositional extremes. The major disadvantage of non-linear subdivision is that it has the potential to generate much larger numbers of compositions (pseudocompounds) for multicomponent solutions resulting in high costs in terms of computational time and memory.

The stretch_factor keyword value cannot be < 0, the default value is 0.0164.

This keyword affects VERTEX, CONVEX, and MEEMUM.

structural_formulae

The structural_formulae keyword controls whether structural formulae are output by WERAMI (in computational mode 1) and MEEMUM.

This keyword may take values: T (true) or F (false). The default is T.

This option only affects WERAMI and MEEMUM.

subdivision_override

The subdivision_override keyword allows users to override the subdivision schemes specified locally in the solution model file with a single global choice.

subdivision_override may take the value: off, stretch, or linear. The default is off.

If subdivision_override = linear, the local values of XMAX, XMIN, and XINC are interpreted as would be the case if IMOD = 0.

If subdivision_override = stretch and IMOD = 0, the local values of XMAX, XMIN, and XINC are interpreted as would be the case if IMOD = 2. If IMOD = 2 or 3 the local values XMAX, XMIN, and XINC are interpreted according to the value of IMOD.

This keyword affects VERTEX and MEEMUM.

T_melt

The T_melt keyword specifies a temperature (K) threshold below which the endmembers of a melt solution model, e.g., melt(HP) and pMELTS(G), are arbitrarily destabilized. This is sometimes helpful because the thermodynamic properties of the melt endmembers do not extrapolate to low temperature. This option only affects melt endmembers that are used by a solution solution model; thus problematic endmembers that are present in the data base being used but not included in a model for a stable melt phase must be excluded explicitly in the problem definition file (the file created by BUILD). The disadvantage of using T_melt > 0 is that it may result in an artificial "solidus" at T = T_melt.

The default value of T_melt is 873.

This keyword affects VERTEX, CONVEX, and MEEMUM.

T_stop

The T_stop keyword specifies a temperature (K) threshold below which chemical equilibration is assumed to cease. If the temperature for a calculation is below the threshold, then the chemical equilibrium is computed at T_stop, but physical properties for the resulting phase assemblage are computed at the nominal temperature.

The default value of T_stop is 0.

This keyword affects VERTEX and MEEMUM.

timing

The timing keyword controls whether VERTEX outputs CPU time usage statistics. When timing is set to T (true), the output is written to the user console and a file named my_project.tim, where my_project is the root of the problem definition file.

This keyword may take values: T (true) or F (false). The default is T.

This option only affects VERTEX.

unbounded_composition (solution model keyword)

NOTE: unbounded_composition is not a perplex_option file keyword, rather it is an option that applies to a specific solution model. To implement this keyword modify the solution model by adding the keyword before the end_of_model keyword.

If the unbounded_composition keyword is present in a solution for which the model composition space is simplicial, then compositions outside the model space are allowed provided they do not violate site fraction constraints and/or mass positivity.

This keyword affects VERTEX and MEEMUM.

variance

The variance keyword specifies the maximum true variance of pseudo-univariant equilibria to be traced during Schreinemakers diagram calculations. Two values are specified, these are applied, respectively, for the exploratory and auto-refine stages of calculation.

This keyword affects CONVEX.

vrh/hs_weighting

The value of the vrh/hs_weighting keyword is the weighting (χ) used to compute aggregate adiabatic elastic moduli for seismic wave-speed calculations according to the averaging scheme

Z = (1-χ)*Z_- + χ*Z₊

where Z_- and Z₊ are the lower and upper bounds on the aggregate modulus. The method (VRH or HS) of computing the bounds is specified by the bounds keyword. For calculations analyzed with WERAMI, changing this keyword does not necessitate repeating the primary calculation with VERTEX.

This keyword takes numeric values (< 12 characters): 0 -> 1. The default value is 0.5.

This option affects WERAMI, MEEMUM and FRENDLY.

Other keywords relevant to seismic velocity calculations: bounds, explicit_bulk_modulus, poisson_ratio, Anderson-Gruneisen, melt_is_fluid, interpolation, seismic_output, seimsic_data_file.

warn_interactive

VERTEX and MEEMUM issue intrusive warnings that identify probable bad practice in the configuration of a problem. After such a warning, the user is offered an interactive Y/N choice. If the user answers affirmatively, then execution continues. Setting warning_interactive to F (false) makes these warnings non-interactive by automatically allowing execution to continue. This setting is NOT recommended except in instances where the user is certain that the problem configuration is legitimate.

This keyword may take values: T (true) or F (false). The default is T.

This keyword affects VERTEX and MEEMUM.

warn_no_limit

To limit the volume of information written to the console during execution, VERTEX and MEEMUM limit the number of times certain warnings may be repeated. Setting warn_no_limit to T (true) overrides these limits for certain warnings.

This keyword may take values: T (true) or F (false). The default is F.

This keyword affects VERTEX and MEEMUM.

warning_ver637

If immiscible compositions of a solution are stable, then WERAMI automatically disables interpolation because of the possibility of interpolating between the wrong compositions. Setting warning_ver637 to F (false) overrides this behavior.

For example: if a feldspar solution model is in use, then three feldspars may coexist. WERAMI distinguishes phase assemblages by the number of compositions of a solution, but not the compositions; thus, if the order in which the immiscible phases are identified is different at two nodes of the computational grid, e.g., feldspar (plagioclase composition) + feldspar (sandine composition) at one node and feldspar (sanidine composition) + feldspar (plagioclase composition) at the other, then WERAMI would interpolate incorrectly between the plagioclase and sandine compositions at the two nodes, resulting in inconsistent compositions and properties for the feldspar phases. Disabling interpolation eliminates the possibility of this error, but often results in blocky data patterns. In general, the ordering of immiscible compositions is consistent between adjacent nodes and therefore the error is unlikely. 

This keyword may take values: T (true) or F (false). The default is T.

This keyword affects WERAMI.

zero_bulk

The zero_bulk keyword specifies the threshold below which a the bulk composition of a component is considered to be zero. This option is useful for processing fractionation calculations because in such calculations the amount of a component may become negligible and destabilize the calculations. Under these conditions, if zero_bulk is set to a finite value, then VERTEX will warn of the potential problem. If zero_bulk is assigned a value of zero the option is effectively off.

This keyword takes numeric values (< 12 characters), 1e-6 is the default value.

This keyword affects VERTEX and MEEMUM.

zero_mode

The zero_mode keyword determines whether stable phases present in zero amount are eliminated from the assemblage on output. This option is particularly useful for processing fractionation calculations because in such calculations the amount of one or more components may become zero. The numerical value assigned to zero_mode defines the tolerance for determining zero amount. If zero_mode is assigned a negative value the option is turned off.

This keyword takes numeric values (< 12 characters): 0 -> 1, 1e-6 is the default value except for fractionation calculations. For fractionation calculations zero_mode defaults (is fixed?) to zero.

This keyword affects VERTEX and MEEMUM.

1d_path

For phase fractionation calculations the 1d_path keyword indicates the number of nodes taken to define the path in the exploratory and auto-refine stages of the calculation. The default values for 1d_path are 20 and 150 for the exploratory and auto-refinement stages of a phase fractionation calculation. As a rule of thumb, the latter value should be chosen such that the results do not change significantly if it is varied by a factor of two.

This keyword affects VERTEX.